4차 방정식(Quartic Equation)의 페라리의 해법과 근의 공식

4차

사차 방정식의 기본꼴은 다음과 같다.

일단, 양변을 a 로 나누면

4차 방정식의 근을 구하려면 일단 3차 방정식과 비슷한 방법으로 3차 항을 없애주어야 한다.
따라서 x 를 다음과 같이 치환하자.

이 때 위를 원래 식에 대입을 하면

 
가 된다. 
이 때 위를 정리하면

 
이 때, α,β,γ 를 다음과 같이 치환하자.

  ,

   ,

 


이를 다시 방정식에 대입하면 준 방정식은

 
이 때
β = 0 인 경우 : 이는 u² 을 x 로 치환한 후, 이차 방정식을 풀면 된다.
γ = 0 인 경우 : 이는 u=0 일 때 해를 가지고 u 로 나눈 후, 3차 방정식을 풀면 된다. 참고적으로 말하자면 이를 depressed cubic 이라고 말하며, 풀이는 간단하다.
( 풀이 참조 : http://kevin0960.tistory.com/entry/3-차-방정식의-근의-공식-카르다노의-해법 )

만약 그렇지 않은 경우,  다음은 Ferrari 의 해법이다.

따라서 위 식에 식 (1) 을 대입하면 아래와 같이 된다.
 
이 때,

이고 ( 전개를 하면 된다.)

이다.  (위 도 마찬가지로 전개 해보면 된다. )
이 때, 위의 두 식을 통해 다음의 식을 유도할 수 있다. ( 위로 두 번째 식의 2yu² 에 위의 식을 대입 )

따라서 이 식을 위의 식 (2) 에 대입한다면

을 얻을 수 있다. 이 때, 우리가 생각해 봐야 할 점은, 우변이 제곱식이 되도록 y 값을 잘 조정해야 한다는 점이다. 따라서 우변이 제곱식이 되게 하는 y 값을 찾아보자.
일단,

이고,

이다. 따라서, (3) 식의 우변을 제곱식으로 만드는 y 는 다음의 방정식을 만족하게 된다.

위 식을 전개하면

이제, 위 식을 다시 정리하면

따라서, 위의 식을 2 로 나눈다면 y 에 대한 3차 방정식이 탄생하게 된다.

이제, 위 식의 두번째 항을 없애기 위해 y 를 다음과 같이 치환하자.

위 치환된 y 를 다시 식에 대입하고 정리하면 다음과 같이 된다.

편의성을 위해 두번째 항과 세번째 항의 계수들을 각각 P,Q 로 치환하자.

따라서 위 방정식은 다음과 같이 바뀐다.

위 방정식은 Depressed Cubic 이라고 부르며, 이에 대한 풀이는 이미 여기서 많이 다루었다. 따라서 여기에서는 식 (4) 를 풀었다고 하자. 이 때, 그 해는 다음과 같다.

이 때, V 와 U 는 각각 다음과 같다.

이제, (5) 를 통한 y 의 값을 통해서 (3) 식의 우변을 제곱식으로 만들 수 있게 되었다.

위 식은 아래식과 같다.

가 된다. 따라서

이제 위 식을 u 를 기준으로 다시 정리하면

이 때, 복호동순이다.
따라서 근의 공식에 대입해서 u 값을 구한 후, u 값을 통해 x 값을 구할 수 있다.

한가지 유의할 점은, 두 개의 는 부호가 같고, 는 달라도 된다.

Ferrari 의 해법을 다시 요약해 본다면, 어떠한 사차방정식

에 대해서, α, β, γ 를 각각 다음과 같이 치환하자.

이 때, β = 0 이라면,

로 유일하고 , β 가 0 이 아니라면, P, Q, R 을 다음과 같이 치환하자.

라 하면,

이고, 편의상 α + 2y 를 W 로 치환하면

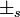이 때, 두 개의  는 부호가 같고, 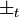는 달라도 된다.