암호학(Cryptography) 의 모든 것

암호학 (Cryptography, 또는 cryptology 라 하는데 이는 그리스어 κρύπτω krýpto 의 '숨겨진' 과 동사 γράφω gráfo "~를 쓰다 " 또는 λέγειν legein "말하다" 에서 유래했다.) 은 숨겨진 정보를 찾아내고 연구하는 학문이다. 현대에선 암호학은 수학과 컴퓨터 공학에 한 갈래로 정보이론(information theory) , 컴퓨터 보안, 그리고 공학과 많은 연관이 있다. 암호학은 현대사회의 필수 불가결한 학문으로 ATM 카드, 컴퓨터 비밀번호, 전자 상거래 등과 같은 부분에서 쓰인다.
암호학에 관련된 용어들
지금까지, 암호학은 주로 '부호화 하는 것(Encryption, 평문을 암호화된 문장으로 바꾸는 것)' 을 가리켰다. 반면에 '복호화(Decryption)' 하는 것은 부호화하는 것의 반대로 어떠한 알수 없는 암호문(ciphertext) 를 평문(plation text) 로 변환하는 것이다. 사이퍼(cipher 또는 cypher 라고도 씀) 는 어떠한 평문을 암호문으로 부호화 하는 것과, 암호문을 평문으로 복호화 하는 것을 하는 알고리즘을 일컫는다. 사이퍼를 통해 부, 복호화 하려면 그에 대한 알고리즘과, 키(key) 가 필요하다. 키는 비밀스러운 매개체로 (오직 암호문을 주고받는 상대자 많이 알고 있다) 부, 복호화 하는데 쓰인다. 키는 매우 중요하며, 키를 이용하지 않는 사이퍼는 매우 쉽게 해독되기 때문에 상당히 효과가 떨어진다.
보통, '코드(code)' 는 어떠한 평문의 부호화 과정이나 숨겨진 뜻을 일컫는 말이다. 하지만 암호학에서는 좀더 깊은 뜻이 들어 있다; 이는 평문의 어떠한 부분을 대체한 것(예를들어 단어, 문장 등) 을 말한다. 예를들어서 '2 개의 애플파이가 새벽에 우리를 공격한다' 라는 평문에서는 '애플파이' 가 코드다. 왜냐하면 '애플파이' 는 '전투기' 를 대체한 말이기 때문이다. 코드는 고도의 암호학에서는 잘 쓰이지 않는다. 하지만 어떠한 지명 같은 것을 가리킬 때 (예를 들어 작전명 오버로드 - Operation Overlord, 이는 노르망디 상륙 작전을 일컫는 말이다.) 는 종종 쓰인다.
영어에서 'cryptography' 와 'cryptology' 는 비슷한 뜻을 지닌다. 하지만 'cryptography' 는 주로 암호화 하는 방법을 가리키는 단어고, 'cryptology' 는 주로 암호화 하는 방법(cryptography) 및 암호 해독학(cryptanalysis)을 모두 지칭하는 말이다.
암호학에서는 종종 언어들의 특성을 연구하기도 한다. 예를들어서 영문 암호문을 해독할 때, 'k' 가 많이 나타났다면 이는 'e' 를 'k' 로 바꾸었다고 생각할 수 있다. 왜냐하면 'e' 는 영어 문장에서 가장 많이 등장하는 알파벳이기 때문이다. 그 외에도 문장의 패턴이라든지 알파벳의 조합이라든지 등을 연구하는데 이를 암호언어학(Cryptolinguistics) 라 한다.
암호학의 역사
현대시대 전에도 암호학은 매우 중요한 역할을 담당했다. 어떠한 메세지를 암호화된 문장으로 바꾸거나 다시 평문으로 바꾸는 작업과 어떠한 메세지가 상대로 전해질 때 비록 중간에 제 3 자(비밀 키를 모르는) 가 가로채더라도 알 수 없게 만드는 기술 등 으로 쓰였다. 최근의 암호학은 위 외에도 메세지의 도청 여부를 판단하거나, 송,수신자의 인증, 디지털 사인, 컴퓨터 보안 등에서 매우 중요한 역할을 담당한다.
초기의 암호화 과정은 단지 펜과 종이만 필요할 정도로 단순하였다. 초기의 사이퍼 종류는 전자 암호법(transposition ciphers) 라 불리는 것으로 이는 메세지의 알파벳의 순서를 뒤섞어 놓는 것이였다. 예를들자면 'help me' 를 전자 암호법으로 부호화 한다면, 'ehpl me' 가 된다. 또한 환자식 암호법(substitution ciphers) 라 불리는 사이퍼는 알파벳들을 다른 알파벳으로 일대일 대응시켜서 부호화 하는 것이다. 예를들자면 'fly at once' 를 부호화 한다면 'gmz bu podf' 가 되며 이는 f 를 g 로, l 을 m 으로 등등 서로 대응시켜 바꾸었다. 한 예로 카이사르는 환자식 암호법으로 이용해 부호화 했는데 각 알파벳을 3칸 앞으로 밀어서 나타냈다. 예를들자면 'I like math' 는 'l olnh pdwk' 로 부호화 되었다.
외교관이나 스파이, 전쟁 지도자들에게는 의사소통시 암호화하는 것이 필수적이였다. 예를들자면 초기의 히브리 사이퍼가 그 예이다. 카마수트라(Kama Sutra, 고대 인도의 힌두 성전) 에는 서로 사랑하는 이들이 남에게 폐를 끼치지 않게 의사소통 할 수 있는 방법으로 암호학을 추천했다. 심층암호(steganography, 메세지의 존재성 조차 숨겨 매우 안전하게 보관한다.) 또한 고대시대 에서 만들어졌다. 예를들면 헤로도투스(Herodotus, 그리스의 역사가)는 노예의 머리를 깍은 후에 비밀 메세지를 세긴 후, 다시 머리를 자라게 해 숨겼다. 요즘에는 보이지 않은 잉크나, 마이크로도트(microdots, 점 크기 만한 미소사진), 디지털 워터마크(digital watermarks, 디지털 워터마크는 디지털 콘텐츠에 사용자만이 알 수 있는 아이디(ID) 또는 정보 등의 부호를 삽입하거나, 영상·음성 등의 신호에 특정한 코드나 유형 등을 삽입하는 기술), 등을 이용해 정보를 숨긴다.
고전의 사이퍼(위에 나와있듯이 환자식 암호법나 전자 암호법 등)를 통한 부호화된 암호문은 언제나 통계학적인 정보를 남겨 이를 통해 암호를 해독할 수 있다. 9세기에 빈도수 분석법(frequency analysis) 이 발견된 이후 대부분의 암호문은 쉽게 해독될 수 있었다. 위와 같은 고전 사이퍼들은 아직도 퍼즐 같은 곳에서 많이 쓰인다. 다중단일문자치환 암호법(polyalphabetic cipher)가 알베르티(Leon Battista Alberti)에 의해 1467년 발명되기 전까지 많은 사이퍼들은 매우 취약했었다. 알베르티가 발명한 다중단일문자치환 암호법은 메세지의각 부분마다 다른 사이퍼를 이용하는것 이였다. 알베르티는 또한 그가 발명한 다중단일문자 치환 암호법을 이용해 자동으로 부호화 해주는 해주는 사이퍼 장비를 발명해 냈다. 1586년에는 프랑스 외교관 비제네르(Blaise de Vigenère) 가 비제네르 암호법(polyalphabetic Vigenère cipher)을 만들었다. 이는 키워드(key word)를 이용한 암호법으로 어떠한 키워드가 이용됬는지에 따라 평문이 다르게 암호화 된다. 1800년대 중반에는 배비지(Babbage)가 비제네르 암호법으로 암호화된 평문은 빈도수 분석법으로 부분적으로 해독할 수 있음을 보였다.
빈도수 분석법이 매우 유용한 해독 테크닉이였지만 암호문은 아직 효과적이였다. 많은 사람들은 빈도수 분석법을 통해 암호를 해독하는 것에 대해선 두려워 하지 않았다. 암호문을 빈도수 분석법을 이용하지 않고 해독하기 위해서는 무슨 사이퍼가 이용되었는지 알아야만했다. 따라서 간첩 행위, 뇌물 수수, 강도 행위 등이 사이퍼를 알아내기 위해 사용되었다. 이는 19세기 들어 더 눈에 띄게 나타났는데 사이퍼의 알고리즘의 경우, 이를 보호할 수 있는 방법이 없었따. 따라서 상대방이 이 암호문의 사이퍼를 정확히 알고 있는 경우라도 암호가 잘 보호되어야만 했다. 따라서 1883년에 오그스트(Auguste Kerckhoffs) 에 의해 'Kerckhoffs 의 원리' 가 만들어 졌고 이는 클라우드(Claude Shannon) 에 의해 'Shannon's Maxim' - '적이 사이퍼를 알 때' 라는 이름으로 보완되었다.
 많은 종류의 기계 장비를 통해서 사이퍼를 이용하는 경우도 많다. 한가지 예를들자면 고대 그리스의 스키테일(scytale) 의 경우 스파르타 인들이 전자 암호법을 이용해 암호화 할 때 쓰였던 도구다. 중세시대에는 사이퍼 그릴(cipher grille) 과 같은 장비가 만들어 졌으며 이는 심층암호화 하기 위해 쓰인다. 다중단일문자치환 암호법이 발명된 이후, 사이퍼 디스크(cipher disk), 요하네스 트리테미우스(Johannes Trithemius)의 tabula recta (사각
많은 종류의 기계 장비를 통해서 사이퍼를 이용하는 경우도 많다. 한가지 예를들자면 고대 그리스의 스키테일(scytale) 의 경우 스파르타 인들이 전자 암호법을 이용해 암호화 할 때 쓰였던 도구다. 중세시대에는 사이퍼 그릴(cipher grille) 과 같은 장비가 만들어 졌으며 이는 심층암호화 하기 위해 쓰인다. 다중단일문자치환 암호법이 발명된 이후, 사이퍼 디스크(cipher disk), 요하네스 트리테미우스(Johannes Trithemius)의 tabula recta (사각  알파벳 테이블로, 각 열은 기
알파벳 테이블로, 각 열은 기
존의 알파벳을 한 칸씩 뒤로 밀어서 나타낸 표이다.) , 토마스 제퍼슨의 멀티 실린더(Thomas Jefferson's multi-cylinder, 1900년대에 바제리에 의해 독립적으로 재 발명된다.) 등이 그 예 이다. 20세기에도 몇몇의 부호화하는 기계장비들이 발명되었다. 예를들면 제 2차 세계대전서 이용되었던 에니그마(Enigma machine)가 그 예이다.
제 2차 세계대전 이후 디지털 컴퓨터와 전자장비 등의 발달에 따라 더욱 복잡한 사이퍼의 이용이 가능해졌다. 게다가 종전의 고전 사이퍼는 오직 문자만을 암호화 할 수 있었던 반면에 컴퓨터는 2진 형식으로 표현된 어떠한 데이터도 암호화 가능해 암호 해독을 위한 언어학적인 접근을 불가시켰다. 고전의 문자나 숫자들을 암호화 했던 고전 사이퍼와는 달리 많은 수의 컴퓨터 사이퍼들은 각각의 이진 비트에 대해 암호화를 한다(때로는 한꺼번해 하기도 한다). 그러나 컴퓨터 사이퍼는 고전 사이퍼에 비해 그 복잡도를 매우 증가시켰고 몇몇의 사이퍼들은 암호화 하기 매우 빠르면서도 효과적이며 해독하려면 오랜 시간이 걸리는 좋은 사이퍼들도 있다.
암호학에 대한 심층있는 연구는 비교적 최근에 시작되었다. 1970년대 후반에 데이타 암호화 기준(DES, the Data Encryption Standard) 가 발표되었고 RSA 알고리즘을 통한 암호화 기법이 탄생하였다. 그 후로 암호학은 통신, 컴퓨터 네트워크, 컴퓨터 보안등에서 매우 널리 쓰이게 되었다. 요즘의 암호화 기법들은 컴퓨터가 계산하기에 시간이 걸리는 것들을 이용하는데 예를들자면 큰 정수의 소인수분해라던지 이산대수(discrete logarithm) 문제 등을 이용한다. 현대의 대다수의 암호화 기법들은 일시패드(OTP, one-time-pad) 기법을 제외하곤 '컴퓨터가 이 문제를 효과적으로 풀지 못할 때에' 라는 사실을 가정하에 안전하다고 한다. 일시패드 암호화 방법은 평문에 대해 패드(pad) 라 불리는 난수 키(여기서 의사 난수가(pseudo random) 이 아닌 완전한 난수) 를 모듈러 연산을 해(2진 데이터의 경우 XOR 연산도 된다) 낸 결과가 암호가 된다. 이 때 난수 키는 딱 한 번 밖에 이용하지 않기 때문에 이런 암호를 가르켜 일시패드(one-time pad) 라 한다. 이는 1917년에 개발되었고 만약 난수 키가 계속 비밀로 지켜진다면 완벽한 보안성(절대로 깰 수 없음) 을 자랑한다. 또한 어떠한 사이퍼가 완벽한 보안성을 가지려면 OTP 키와 같은 키가 반드시 필요하다는 사실도 증명되었다.
 암호화 알고리즘을 개발하는 사람들은 반드시 먼 미래에 암호를 해독하는 데 쓰이는 장치를 염두에 두고 만들어야 한다. 예를 들자면 컴퓨터의 엄청난 계산능력을 통해 암호를 해독하기 위한 무차별 대입 공격(brute-force attacks) 가 수월해 졌다. 또한 미래에 개발된 양자 컴퓨터의 엄청난 연산능력은 RSA 암호방식에 쓰이는 큰 수의 소인수 분해를 현존의 컴퓨터 보다 훨씬 빠른 속도로 해낼 수 있으리라 본다.
암호화 알고리즘을 개발하는 사람들은 반드시 먼 미래에 암호를 해독하는 데 쓰이는 장치를 염두에 두고 만들어야 한다. 예를 들자면 컴퓨터의 엄청난 계산능력을 통해 암호를 해독하기 위한 무차별 대입 공격(brute-force attacks) 가 수월해 졌다. 또한 미래에 개발된 양자 컴퓨터의 엄청난 연산능력은 RSA 암호방식에 쓰이는 큰 수의 소인수 분해를 현존의 컴퓨터 보다 훨씬 빠른 속도로 해낼 수 있으리라 본다.
20세기 전까지 암호학은 암호화된 문장의 언어학 적인 패턴을 찾는데 주력하였다. 하짐나 현재의 암호학은 수학, 정보이론, 컴퓨터 공학, 통계학, 조합론, 추상 대수학, 정수론 까지 모두 포괄되는 내용이 되었다. 뿐만아니라 암호학은 공학에서의 하나의 분야이다. 또한 암호학적인 문제들과 양자역학과의 관계를 연구하는 것도 열띄게 연구되고 있다.
현대의 암호학
1. 대칭키 암호화(Symmetric-key cryptography)
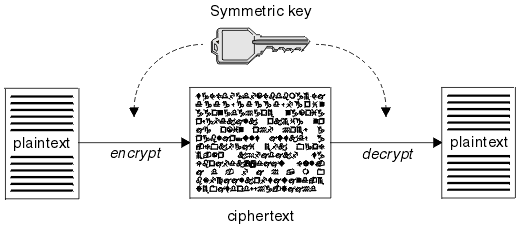 대칭키 암호화는 송,수신자가 똑같은 키를 사용하여 부,복호화 하는 것을 말한다(키가 서로 다를 수 도 있지만 약간의 계산만 한다면 구할 수 있는 상태이다). 이는 1976년도 까지 공공연하게 알려져 있던 암호화 방법 이였다.
대칭키 암호화는 송,수신자가 똑같은 키를 사용하여 부,복호화 하는 것을 말한다(키가 서로 다를 수 도 있지만 약간의 계산만 한다면 구할 수 있는 상태이다). 이는 1976년도 까지 공공연하게 알려져 있던 암호화 방법 이였다.
현대 암호학에서 대칭키 사이퍼에 대한 연구는 주로 블록 사이퍼(block ciphers) 와 스트림 사이퍼(stream ciphers) 로 한다. 블록 사이퍼는 알베르티의 다중단일문자치환 암호법이 더 구체화 된 것 이라 볼 수 있다. 블록 사이퍼는 평문의 한 부분을 키로 택한 후, 똑같은 크기의 암호문으로 암호화 한다. 메세지들이 대부분 크기가 한 블록 이상 되기 때문에 각 블록들을 잘 맞추는 것도 필요하다. 몇가지 방법들이 개발되었고 몇몇 들은 다른 것 보다 높은 보안성을 자랑한다.
데이타 암호화 구격(DES,Data Encryption Standard) 와 고급 암호화 표준(AES, Advanced Encryption Standard) 는 미 정부 암호화 구격에 따라 지정된 블록 사이퍼 디자인 기준이다. (결국에는 DES 가 아닌 AES 가 공식적으로 채택되었다) 비록 DES 는 공식적으로 지정된 표준이 아니였지만, 아직도 꽤 많은 곳에서 쓰이고 있다. 예를들자면 ATM 암호화나, 이메일, 보안 원격 접속 등이 그 예이다. 많은 종류의 블록 사이퍼들이 개발되고 발표되었지만 많은 블록사이퍼들은 쉽게 해독 수 있다.
스트림 사이퍼는 블록 사이퍼와는 반대로, 매우 긴 스트림 키를 만들어 평문에 비트 대 비트 아니면 문자 대 문자 단위로 마치 일시패드 기법 처럼 결합시킨다. 스트림 사이퍼 에서는 출력 스트림은 사이퍼가 작동할 때 마다 바뀌는 내부 상태에 따라 달라진다. 내부 상태의 변화는 오직 키에 의해 결정되며 몇몇의 스트림 사이퍼와 평문 스트림도 마찬가지 이다. RC4 는 가장 잘 알려진 스트림 사이퍼이다 .
해시 함수(Cryptographic hash functions, message digest functions 라 불리기도 한다) 는 키가 필요 없으며 단지 암호화 알고리즘에 관련이 있다. 그 함수들은 데이타를 받아들이고(종종 전체 메세지로 이용한다), 짧은 해시 값을 내보낸다. 두 개의 평문이 똑같은 해시값을 내보내는 일(collsions) 은 매우 발생하기 힘들다.
메세지 인증 코드(Message Authentication codes, MACs) 는 암호화 된 해시 함수들과 비슷하며 단지 해시 값을 인증하기 위해 비밀 키를 이용한다는 점만 다르다.
2. 공개 키 암호화(Public-key cryptography)
대칭키 암호화는 가장 큰 단점은 통신 네트워크 상의 멤버들 수가 증가할 수 록 필요한 키의 수는 제곱에 비례해 보안성을 위한 키 관리를 매우 어렵게 만든다. 게다가 서로 통신시 서로간에 키를 안전하게 알려줄 수 있는 방법이 없다면 닭-달걀 문제(chicken-and-egg problem, 닭은 알을 낳지만, 알은 닭을 부화시킨다. 따라서 어느 것이 더 먼저 만들어 졌을까? 하는 문제이다.) 를 발생시켜 암호학계에 커다란 장애물이 되었다.
1976년에 학계에 놀라운 발표가 있었다. 위트필드 디피(Whitfield Diffie) 마틴 헬먼(Martin Hellman)은 공개키(public key, 포괄적으로 보자면 비대칭키(asymmetric key)라 볼 수 있다. ) 라는 것을 발표했는데 이는 공개키와 개인키(private key)가 서로 다르지만 수학적인 연관이 있어 이를 이용하는 것이였다. 공개키 시스템은 비록 한 키로 부호화 한다면 다른 키 만이 복호 가능하도록 만들어 졌다. 대신에 두 키는 비밀스럽게 밀접한 관계를 맺으며 생성된다. 역사가 데이비드 칸(David Kahn)은 공개키 암호화를 "다중단일문자치환 암호법 다음으로 암호학계에 새로운 혁명을 일으킨 암호법" 이라고 했다.
공개키 암호화 시스템에선 공개키는 다른 사람들에게 알려져도 되지만, 공개키와 동시에 비밀스럽게 생성된 개인키는 반드시 비밀로 남아있어야 한다. 공개키는 주로 부호화 할때 쓰이며, 개인키는 주로 복호화 할 때 쓰인다. 디피와 헬먼은 공개키 암호화가 디피-헬먼 키 교환 프로토콜(Diffie-Hellman key exchange protocol) 을 통해 실현 가능성을 보였다.

1978년에 리베스트(Ronald Rivest), 샤미르(Adi Shamir), 애들만(Len Adleman) 은 또다른 공개키 암호화 시스템인 RSA(개발한 수학자의 머리글자를 따서 이름을 지음) 를 발명했다. 디피-헬만과, RSA 알고리즘은 높은 보안성을 띈 공개키 사이퍼이며 이는 전세계에서 가장 많이 쓰이는 사이퍼다. 그 외에도 공개키 사이퍼로는 Cramer-Shoup 암호체계, ElGamel 암호, 그리고 여러 종류의 타원 곡선 암호화 기법들이 있다.
공개키 암호화는 디지털 서명 체계로도 사용할 수 있다. 디지털 서명은 우리가 흔히 말하는 서명과 똑같은 성질을 띄고 있다; 자신의 것은 쓰기는 쉽지만 다른 사람의 것을 따라하기는 힘들 다는 점이다. 디지털 서명은 영구적으로 초기에 서명된 문서에 영구적으로 결합된다. 이 말은 디지털 서명은 그 문서 전체를 암호화 하지는 않으며 제 3자가 그 문서의 내용을 볼 수 는 있지만 그 문서가 누구로 부터 왔는지에 대한 정보는 사라지지도 바뀌지도 않는 다는 점이다. 디지털 서명 체계이는 두 개의 알고리즘이 쓰인다. 첫번째로는 서명을 위해 비밀키(또는 메세지의 해시값) 이 사용되며 두번째로는 인증을 위한 것으로 공개키가 서명의 정당성을 검사하기 위해 사용된다. RSA 와 DSA(Digital Signature Algorithm, 디지털 서명 알고리즘) 가 주로 사용된다.
공개키 알고리즘은 보통 전산학적으로 계산하기 어려운 정수론 문제들을 기반한다. 예를들자면 RSA는 큰 정수의 소인수 분해에 난해성을 기반으로 하며, 디피-헬먼 과 DSA 는 이산 대수문제의 난해성을 기반으로 한다. 최근에 개발된 타원 곡선 암호화기법은 타원곡선을 이용한 복잡한 문제를 기반으로 개발되었다. 위에 나열된 문제들은 어떤 수에 대한 모듈로(modular) 연산과 지수 연산 같은 것들을 기반으로 하기 때문에 전산학적으로 블록 사이퍼보다 시간이 오래걸린다. 따라서 공개키 암호체계는 주로 복합 암호체계(hybrid cryptosystems)를 사용하한다. 복합 암호체계선 주로 메세지를 암호화 속도가 빠른 대칭키 알고리즘을 이용해 암호화 하며 이 때 이용되는 키는 공개키 알고리즘을 이용해서 암호화 되어서 보내진다.
 암호에 대한 가장 큰 오해는 모든 암호문은 해독될 수 있다는 것이다. 하지만 벨 연구소(Bell Labs) 에 소속된 클라우드는 일시패드 사이퍼는 키가 만약 완전한 난수이며 다시 재사용되지 않고 어떠한 공격자들에게서도 비밀로 유지된다면 일시패드 사이퍼를 통해 암호화된 평문은 결코 해독될 수 없음을 증명하였따. 하지만 일시패드가 아닌 대부분의 사이퍼들은 무차별 대입 공격을 통해서 해독될 수 있으나 키의 크기가 커지면 커질수록 무차별 대입을 통해 해독하는데 걸리는 시간은 지수적으로 커진다. 현재까지 알려진 사이퍼 중 일시패드 사이퍼만이 이론상으로 결코 깨질 수 없는 사이퍼이다.
암호에 대한 가장 큰 오해는 모든 암호문은 해독될 수 있다는 것이다. 하지만 벨 연구소(Bell Labs) 에 소속된 클라우드는 일시패드 사이퍼는 키가 만약 완전한 난수이며 다시 재사용되지 않고 어떠한 공격자들에게서도 비밀로 유지된다면 일시패드 사이퍼를 통해 암호화된 평문은 결코 해독될 수 없음을 증명하였따. 하지만 일시패드가 아닌 대부분의 사이퍼들은 무차별 대입 공격을 통해서 해독될 수 있으나 키의 크기가 커지면 커질수록 무차별 대입을 통해 해독하는데 걸리는 시간은 지수적으로 커진다. 현재까지 알려진 사이퍼 중 일시패드 사이퍼만이 이론상으로 결코 깨질 수 없는 사이퍼이다.
암호 해독을 하기 위해선 여러 종류의 방법이 사용되며 이는 다음과 같이 종류를 나눌 수 있다. 암호문 공격(ciphertext-only attack) 은 암호 해독가들이암호문들의 집합에만 오직 접근 가능하다는 것을 가정한 상태에서의 공격 방법이다.(현대의 좋은 암호체계는 이 암호문 공격에 당할 염려가 없다.) 알려진 평문 공격(known-plaintext attack)은 공격자가 평문과 암호문의 샘플을 가지고 있고 더 많은 정보(예를들자면 비밀키)를 알기위해 자유롭게 평문과 암호문에 대해 공격이 가능할 수 있는 공격 방법이다. 선택된 평문 공격(chosen-plaintext attack) 에서는 공격자가 평문과 이에 상응하는 암호문들을 가졌을 때의 공격방법이다. 한 예로 영국군이 독일군의 암호를 해독하기 위해 사용했던 Gardening 이란 작전도 이에 포함된다. 마지막으로 선택된 암호문 공격(chosen-ciphertext attack)은 공격자가 암호문을 고르고 이에 상응하는 평문을 알 때 사용하는 기법이다.
공개피 알고리즘은 앞에서 설명했듯이 전산학적으로 계산하기 힘든 문제에 기초를 둔다. 예를들자면 가장 유명한 것으로 큰 정수의 소인수 분해의 난해성(RSA 암호) 에 기초를 두거나 이산 대수문제의 난해성을 둔 암호들 도 있다. 따라서 공개키 암호의 해독은 컴퓨터를 통해서 더 빠르게, 효과적으로 계산하는 것이 필요하다. 예를들자면 현재까지 알려진 타원 곡선을 기반으로한 이산 대수 문제를 푸는 알고리즘은 현재까지 알려진 가장 빠른 소인수분해 알고리즘 보다 더 오래 걸리기 때문에 소인수분해 기반 사이퍼들은 타원 곡선 사이퍼 보다 더 큰 키를 이용한다. 따라서 계산 능력이 좀 떨어지는 소형 장비들은 RSA 암호보다 타원 곡선 암호를 이용하기 때문에 1990년대 중반 부터 유명세를 띄기 시작했다.
순수 암호 해독가들은 알고리즘 자체의 취약점을 이용해 암호를 해독하지만 다른 종류의 공격으로는 그 암호화 하는 장비 자체를 공격하는 것으로 'side-channel attacks' 라 부른다. 만약에 공격자가 예를들자면 장비가 암호화 할 평문들의 숫자에 접근이 가능하거나, 장비에게 비밀번호나 PIN 문자에 대한 오류 보고가 가능할 때, 공격자는 시이퍼를 뚫기 위한 타이밍 공격(timing attack) 이 가능하다. 또한 공격자가 중요 정보를 얻기 위해 전달되는 메세지 길이나, 패턴 등을 알아내는 것을 트래픽 분석(traffic analysis) 라 한다. 또한 그 암호하는 사람을 통해서 (절도, 강탈, 공갈, 간첩행위 등을 통해) 알아내는 방법도 있는데 여태까지 나열 한 방법 중 가장 효과적인 방법이라 볼 수 있다.
마치며...
암호학은 현대사회에서 매우 중요한 부분을 담당하고 있는 학문이다. 우리가 지금 인터넷을 쓰고 있는 상황에서도 수많은 정보가 부,복호화 되고 있으며 어디선가는 3자에 의해 해독되고 일지도 모른다(많은 수의 음모론자들은 NSA가 모두 도청해 해독한다고 한다). 뿐만 아니라 옥션 해킹 사건 처럼 보안에 대해서 취약한다면 자신의 개인정보가 모두 유출 될 지도 모른다. 따라서 우리는 암호학에 대한 관심을 가지고 보안에 신경써야 할 필요가 있다.
위 적은 내용(솔직히 번역한 나도 모르는 부분이 많다) 을 모두 알 필요는 없지만 암호사에 대한 간략한 내용과 우리가 쓰는 암호들의 종류, 그리고 전자 상거래 같은 중요한 기밀 자료 전달시에 사용되는 암호들이 무엇인지 아는 것은 필요하다고 생각한다.
참고자료
http://en.wikipedia.org/wiki/Cryptography (기본적으로 이 사이트의 내용을 통 번역했음)
그 외 사진을 찾은 수많은 인터넷 사이트들
우리말이 사전에 없는 단어들은 다른 사람이 쓴 단어를 사용함.
5/5 ~ 5/11 에 걸쳐 1주일간 번역함.

암호학 (Cryptography, 또는 cryptology 라 하는데 이는 그리스어 κρύπτω krýpto 의 '숨겨진' 과 동사 γράφω gráfo "~를 쓰다 " 또는 λέγειν legein "말하다" 에서 유래했다.) 은 숨겨진 정보를 찾아내고 연구하는 학문이다. 현대에선 암호학은 수학과 컴퓨터 공학에 한 갈래로 정보이론(information theory) , 컴퓨터 보안, 그리고 공학과 많은 연관이 있다. 암호학은 현대사회의 필수 불가결한 학문으로 ATM 카드, 컴퓨터 비밀번호, 전자 상거래 등과 같은 부분에서 쓰인다.
암호학에 관련된 용어들
지금까지, 암호학은 주로 '부호화 하는 것(Encryption, 평문을 암호화된 문장으로 바꾸는 것)' 을 가리켰다. 반면에 '복호화(Decryption)' 하는 것은 부호화하는 것의 반대로 어떠한 알수 없는 암호문(ciphertext) 를 평문(plation text) 로 변환하는 것이다. 사이퍼(cipher 또는 cypher 라고도 씀) 는 어떠한 평문을 암호문으로 부호화 하는 것과, 암호문을 평문으로 복호화 하는 것을 하는 알고리즘을 일컫는다. 사이퍼를 통해 부, 복호화 하려면 그에 대한 알고리즘과, 키(key) 가 필요하다. 키는 비밀스러운 매개체로 (오직 암호문을 주고받는 상대자 많이 알고 있다) 부, 복호화 하는데 쓰인다. 키는 매우 중요하며, 키를 이용하지 않는 사이퍼는 매우 쉽게 해독되기 때문에 상당히 효과가 떨어진다.
보통, '코드(code)' 는 어떠한 평문의 부호화 과정이나 숨겨진 뜻을 일컫는 말이다. 하지만 암호학에서는 좀더 깊은 뜻이 들어 있다; 이는 평문의 어떠한 부분을 대체한 것(예를들어 단어, 문장 등) 을 말한다. 예를들어서 '2 개의 애플파이가 새벽에 우리를 공격한다' 라는 평문에서는 '애플파이' 가 코드다. 왜냐하면 '애플파이' 는 '전투기' 를 대체한 말이기 때문이다. 코드는 고도의 암호학에서는 잘 쓰이지 않는다. 하지만 어떠한 지명 같은 것을 가리킬 때 (예를 들어 작전명 오버로드 - Operation Overlord, 이는 노르망디 상륙 작전을 일컫는 말이다.) 는 종종 쓰인다.
영어에서 'cryptography' 와 'cryptology' 는 비슷한 뜻을 지닌다. 하지만 'cryptography' 는 주로 암호화 하는 방법을 가리키는 단어고, 'cryptology' 는 주로 암호화 하는 방법(cryptography) 및 암호 해독학(cryptanalysis)을 모두 지칭하는 말이다.
암호학에서는 종종 언어들의 특성을 연구하기도 한다. 예를들어서 영문 암호문을 해독할 때, 'k' 가 많이 나타났다면 이는 'e' 를 'k' 로 바꾸었다고 생각할 수 있다. 왜냐하면 'e' 는 영어 문장에서 가장 많이 등장하는 알파벳이기 때문이다. 그 외에도 문장의 패턴이라든지 알파벳의 조합이라든지 등을 연구하는데 이를 암호언어학(Cryptolinguistics) 라 한다.
암호학의 역사
현대시대 전에도 암호학은 매우 중요한 역할을 담당했다. 어떠한 메세지를 암호화된 문장으로 바꾸거나 다시 평문으로 바꾸는 작업과 어떠한 메세지가 상대로 전해질 때 비록 중간에 제 3 자(비밀 키를 모르는) 가 가로채더라도 알 수 없게 만드는 기술 등 으로 쓰였다. 최근의 암호학은 위 외에도 메세지의 도청 여부를 판단하거나, 송,수신자의 인증, 디지털 사인, 컴퓨터 보안 등에서 매우 중요한 역할을 담당한다.
초기의 암호화 과정은 단지 펜과 종이만 필요할 정도로 단순하였다. 초기의 사이퍼 종류는 전자 암호법(transposition ciphers) 라 불리는 것으로 이는 메세지의 알파벳의 순서를 뒤섞어 놓는 것이였다. 예를들자면 'help me' 를 전자 암호법으로 부호화 한다면, 'ehpl me' 가 된다. 또한 환자식 암호법(substitution ciphers) 라 불리는 사이퍼는 알파벳들을 다른 알파벳으로 일대일 대응시켜서 부호화 하는 것이다. 예를들자면 'fly at once' 를 부호화 한다면 'gmz bu podf' 가 되며 이는 f 를 g 로, l 을 m 으로 등등 서로 대응시켜 바꾸었다. 한 예로 카이사르는 환자식 암호법으로 이용해 부호화 했는데 각 알파벳을 3칸 앞으로 밀어서 나타냈다. 예를들자면 'I like math' 는 'l olnh pdwk' 로 부호화 되었다.

디지털 워터마크(Digital watermarks), 가운데 Brian Kell 2008 이 워터마크다. |

마이크로도트 카메라(microdot camera) |
외교관이나 스파이, 전쟁 지도자들에게는 의사소통시 암호화하는 것이 필수적이였다. 예를들자면 초기의 히브리 사이퍼가 그 예이다. 카마수트라(Kama Sutra, 고대 인도의 힌두 성전) 에는 서로 사랑하는 이들이 남에게 폐를 끼치지 않게 의사소통 할 수 있는 방법으로 암호학을 추천했다. 심층암호(steganography, 메세지의 존재성 조차 숨겨 매우 안전하게 보관한다.) 또한 고대시대 에서 만들어졌다. 예를들면 헤로도투스(Herodotus, 그리스의 역사가)는 노예의 머리를 깍은 후에 비밀 메세지를 세긴 후, 다시 머리를 자라게 해 숨겼다. 요즘에는 보이지 않은 잉크나, 마이크로도트(microdots, 점 크기 만한 미소사진), 디지털 워터마크(digital watermarks, 디지털 워터마크는 디지털 콘텐츠에 사용자만이 알 수 있는 아이디(ID) 또는 정보 등의 부호를 삽입하거나, 영상·음성 등의 신호에 특정한 코드나 유형 등을 삽입하는 기술), 등을 이용해 정보를 숨긴다.

비제네르(Blaise de Vigenère) |

알베르티(Leon Battista Alberti) |
고전의 사이퍼(위에 나와있듯이 환자식 암호법나 전자 암호법 등)를 통한 부호화된 암호문은 언제나 통계학적인 정보를 남겨 이를 통해 암호를 해독할 수 있다. 9세기에 빈도수 분석법(frequency analysis) 이 발견된 이후 대부분의 암호문은 쉽게 해독될 수 있었다. 위와 같은 고전 사이퍼들은 아직도 퍼즐 같은 곳에서 많이 쓰인다. 다중단일문자치환 암호법(polyalphabetic cipher)가 알베르티(Leon Battista Alberti)에 의해 1467년 발명되기 전까지 많은 사이퍼들은 매우 취약했었다. 알베르티가 발명한 다중단일문자치환 암호법은 메세지의각 부분마다 다른 사이퍼를 이용하는것 이였다. 알베르티는 또한 그가 발명한 다중단일문자 치환 암호법을 이용해 자동으로 부호화 해주는 해주는 사이퍼 장비를 발명해 냈다. 1586년에는 프랑스 외교관 비제네르(Blaise de Vigenère) 가 비제네르 암호법(polyalphabetic Vigenère cipher)을 만들었다. 이는 키워드(key word)를 이용한 암호법으로 어떠한 키워드가 이용됬는지에 따라 평문이 다르게 암호화 된다. 1800년대 중반에는 배비지(Babbage)가 비제네르 암호법으로 암호화된 평문은 빈도수 분석법으로 부분적으로 해독할 수 있음을 보였다.

오그스트(Auguste Kerckhoffs) |

클라우드(Claude Shannon) |
빈도수 분석법이 매우 유용한 해독 테크닉이였지만 암호문은 아직 효과적이였다. 많은 사람들은 빈도수 분석법을 통해 암호를 해독하는 것에 대해선 두려워 하지 않았다. 암호문을 빈도수 분석법을 이용하지 않고 해독하기 위해서는 무슨 사이퍼가 이용되었는지 알아야만했다. 따라서 간첩 행위, 뇌물 수수, 강도 행위 등이 사이퍼를 알아내기 위해 사용되었다. 이는 19세기 들어 더 눈에 띄게 나타났는데 사이퍼의 알고리즘의 경우, 이를 보호할 수 있는 방법이 없었따. 따라서 상대방이 이 암호문의 사이퍼를 정확히 알고 있는 경우라도 암호가 잘 보호되어야만 했다. 따라서 1883년에 오그스트(Auguste Kerckhoffs) 에 의해 'Kerckhoffs 의 원리' 가 만들어 졌고 이는 클라우드(Claude Shannon) 에 의해 'Shannon's Maxim' - '적이 사이퍼를 알 때' 라는 이름으로 보완되었다.


존의 알파벳을 한 칸씩 뒤로 밀어서 나타낸 표이다.) , 토마스 제퍼슨의 멀티 실린더(Thomas Jefferson's multi-cylinder, 1900년대에 바제리에 의해 독립적으로 재 발명된다.) 등이 그 예 이다. 20세기에도 몇몇의 부호화하는 기계장비들이 발명되었다. 예를들면 제 2차 세계대전서 이용되었던 에니그마(Enigma machine)가 그 예이다.
제 2차 세계대전 이후 디지털 컴퓨터와 전자장비 등의 발달에 따라 더욱 복잡한 사이퍼의 이용이 가능해졌다. 게다가 종전의 고전 사이퍼는 오직 문자만을 암호화 할 수 있었던 반면에 컴퓨터는 2진 형식으로 표현된 어떠한 데이터도 암호화 가능해 암호 해독을 위한 언어학적인 접근을 불가시켰다. 고전의 문자나 숫자들을 암호화 했던 고전 사이퍼와는 달리 많은 수의 컴퓨터 사이퍼들은 각각의 이진 비트에 대해 암호화를 한다(때로는 한꺼번해 하기도 한다). 그러나 컴퓨터 사이퍼는 고전 사이퍼에 비해 그 복잡도를 매우 증가시켰고 몇몇의 사이퍼들은 암호화 하기 매우 빠르면서도 효과적이며 해독하려면 오랜 시간이 걸리는 좋은 사이퍼들도 있다.
암호학에 대한 심층있는 연구는 비교적 최근에 시작되었다. 1970년대 후반에 데이타 암호화 기준(DES, the Data Encryption Standard) 가 발표되었고 RSA 알고리즘을 통한 암호화 기법이 탄생하였다. 그 후로 암호학은 통신, 컴퓨터 네트워크, 컴퓨터 보안등에서 매우 널리 쓰이게 되었다. 요즘의 암호화 기법들은 컴퓨터가 계산하기에 시간이 걸리는 것들을 이용하는데 예를들자면 큰 정수의 소인수분해라던지 이산대수(discrete logarithm) 문제 등을 이용한다. 현대의 대다수의 암호화 기법들은 일시패드(OTP, one-time-pad) 기법을 제외하곤 '컴퓨터가 이 문제를 효과적으로 풀지 못할 때에' 라는 사실을 가정하에 안전하다고 한다. 일시패드 암호화 방법은 평문에 대해 패드(pad) 라 불리는 난수 키(여기서 의사 난수가(pseudo random) 이 아닌 완전한 난수) 를 모듈러 연산을 해(2진 데이터의 경우 XOR 연산도 된다) 낸 결과가 암호가 된다. 이 때 난수 키는 딱 한 번 밖에 이용하지 않기 때문에 이런 암호를 가르켜 일시패드(one-time pad) 라 한다. 이는 1917년에 개발되었고 만약 난수 키가 계속 비밀로 지켜진다면 완벽한 보안성(절대로 깰 수 없음) 을 자랑한다. 또한 어떠한 사이퍼가 완벽한 보안성을 가지려면 OTP 키와 같은 키가 반드시 필요하다는 사실도 증명되었다.

전자프론티어재단(EFF, Electronic Frontier Foundation) 의 $250,000 짜리 DES 공격 기기는 1800개의 특별 제작된 칩을 장착하고 며칠 만에 DES 키를 해독할 수 있다.
20세기 전까지 암호학은 암호화된 문장의 언어학 적인 패턴을 찾는데 주력하였다. 하짐나 현재의 암호학은 수학, 정보이론, 컴퓨터 공학, 통계학, 조합론, 추상 대수학, 정수론 까지 모두 포괄되는 내용이 되었다. 뿐만아니라 암호학은 공학에서의 하나의 분야이다. 또한 암호학적인 문제들과 양자역학과의 관계를 연구하는 것도 열띄게 연구되고 있다.
현대의 암호학
1. 대칭키 암호화(Symmetric-key cryptography)

대칭키 암호화 기법의
현대 암호학에서 대칭키 사이퍼에 대한 연구는 주로 블록 사이퍼(block ciphers) 와 스트림 사이퍼(stream ciphers) 로 한다. 블록 사이퍼는 알베르티의 다중단일문자치환 암호법이 더 구체화 된 것 이라 볼 수 있다. 블록 사이퍼는 평문의 한 부분을 키로 택한 후, 똑같은 크기의 암호문으로 암호화 한다. 메세지들이 대부분 크기가 한 블록 이상 되기 때문에 각 블록들을 잘 맞추는 것도 필요하다. 몇가지 방법들이 개발되었고 몇몇 들은 다른 것 보다 높은 보안성을 자랑한다.
데이타 암호화 구격(DES,Data Encryption Standard) 와 고급 암호화 표준(AES, Advanced Encryption Standard) 는 미 정부 암호화 구격에 따라 지정된 블록 사이퍼 디자인 기준이다. (결국에는 DES 가 아닌 AES 가 공식적으로 채택되었다) 비록 DES 는 공식적으로 지정된 표준이 아니였지만, 아직도 꽤 많은 곳에서 쓰이고 있다. 예를들자면 ATM 암호화나, 이메일, 보안 원격 접속 등이 그 예이다. 많은 종류의 블록 사이퍼들이 개발되고 발표되었지만 많은 블록사이퍼들은 쉽게 해독 수 있다.
스트림 사이퍼는 블록 사이퍼와는 반대로, 매우 긴 스트림 키를 만들어 평문에 비트 대 비트 아니면 문자 대 문자 단위로 마치 일시패드 기법 처럼 결합시킨다. 스트림 사이퍼 에서는 출력 스트림은 사이퍼가 작동할 때 마다 바뀌는 내부 상태에 따라 달라진다. 내부 상태의 변화는 오직 키에 의해 결정되며 몇몇의 스트림 사이퍼와 평문 스트림도 마찬가지 이다. RC4 는 가장 잘 알려진 스트림 사이퍼이다 .

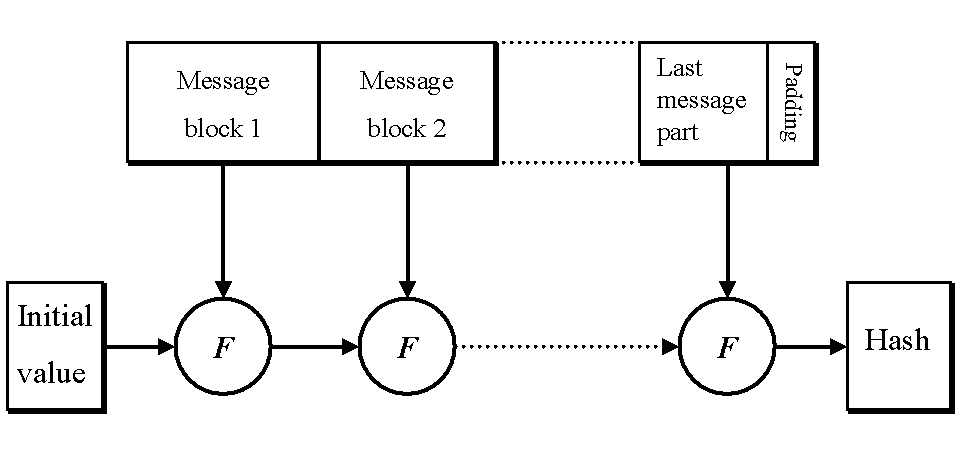
해시 함수
해시 함수(Cryptographic hash functions, message digest functions 라 불리기도 한다) 는 키가 필요 없으며 단지 암호화 알고리즘에 관련이 있다. 그 함수들은 데이타를 받아들이고(종종 전체 메세지로 이용한다), 짧은 해시 값을 내보낸다. 두 개의 평문이 똑같은 해시값을 내보내는 일(collsions) 은 매우 발생하기 힘들다.
메세지 인증 코드(Message Authentication codes, MACs) 는 암호화 된 해시 함수들과 비슷하며 단지 해시 값을 인증하기 위해 비밀 키를 이용한다는 점만 다르다.
2. 공개 키 암호화(Public-key cryptography)
대칭키 암호화는 가장 큰 단점은 통신 네트워크 상의 멤버들 수가 증가할 수 록 필요한 키의 수는 제곱에 비례해 보안성을 위한 키 관리를 매우 어렵게 만든다. 게다가 서로 통신시 서로간에 키를 안전하게 알려줄 수 있는 방법이 없다면 닭-달걀 문제(chicken-and-egg problem, 닭은 알을 낳지만, 알은 닭을 부화시킨다. 따라서 어느 것이 더 먼저 만들어 졌을까? 하는 문제이다.) 를 발생시켜 암호학계에 커다란 장애물이 되었다.

위트필드 디피(Whitfield Diffie) |

마틴 헬먼(Martin Hellman) |
1976년에 학계에 놀라운 발표가 있었다. 위트필드 디피(Whitfield Diffie) 마틴 헬먼(Martin Hellman)은 공개키(public key, 포괄적으로 보자면 비대칭키(asymmetric key)라 볼 수 있다. ) 라는 것을 발표했는데 이는 공개키와 개인키(private key)가 서로 다르지만 수학적인 연관이 있어 이를 이용하는 것이였다. 공개키 시스템은 비록 한 키로 부호화 한다면 다른 키 만이 복호 가능하도록 만들어 졌다. 대신에 두 키는 비밀스럽게 밀접한 관계를 맺으며 생성된다. 역사가 데이비드 칸(David Kahn)은 공개키 암호화를 "다중단일문자치환 암호법 다음으로 암호학계에 새로운 혁명을 일으킨 암호법" 이라고 했다.
공개키 암호화 시스템에선 공개키는 다른 사람들에게 알려져도 되지만, 공개키와 동시에 비밀스럽게 생성된 개인키는 반드시 비밀로 남아있어야 한다. 공개키는 주로 부호화 할때 쓰이며, 개인키는 주로 복호화 할 때 쓰인다. 디피와 헬먼은 공개키 암호화가 디피-헬먼 키 교환 프로토콜(Diffie-Hellman key exchange protocol) 을 통해 실현 가능성을 보였다.

샤미르(Adi Shamir),로날드 리베스트(Ronald Rivest), 애들만(Len Adleman)
1978년에 리베스트(Ronald Rivest), 샤미르(Adi Shamir), 애들만(Len Adleman) 은 또다른 공개키 암호화 시스템인 RSA(개발한 수학자의 머리글자를 따서 이름을 지음) 를 발명했다. 디피-헬만과, RSA 알고리즘은 높은 보안성을 띈 공개키 사이퍼이며 이는 전세계에서 가장 많이 쓰이는 사이퍼다. 그 외에도 공개키 사이퍼로는 Cramer-Shoup 암호체계, ElGamel 암호, 그리고 여러 종류의 타원 곡선 암호화 기법들이 있다.
공개키 암호화는 디지털 서명 체계로도 사용할 수 있다. 디지털 서명은 우리가 흔히 말하는 서명과 똑같은 성질을 띄고 있다; 자신의 것은 쓰기는 쉽지만 다른 사람의 것을 따라하기는 힘들 다는 점이다. 디지털 서명은 영구적으로 초기에 서명된 문서에 영구적으로 결합된다. 이 말은 디지털 서명은 그 문서 전체를 암호화 하지는 않으며 제 3자가 그 문서의 내용을 볼 수 는 있지만 그 문서가 누구로 부터 왔는지에 대한 정보는 사라지지도 바뀌지도 않는 다는 점이다. 디지털 서명 체계이는 두 개의 알고리즘이 쓰인다. 첫번째로는 서명을 위해 비밀키(또는 메세지의 해시값) 이 사용되며 두번째로는 인증을 위한 것으로 공개키가 서명의 정당성을 검사하기 위해 사용된다. RSA 와 DSA(Digital Signature Algorithm, 디지털 서명 알고리즘) 가 주로 사용된다.
공개키 알고리즘은 보통 전산학적으로 계산하기 어려운 정수론 문제들을 기반한다. 예를들자면 RSA는 큰 정수의 소인수 분해에 난해성을 기반으로 하며, 디피-헬먼 과 DSA 는 이산 대수문제의 난해성을 기반으로 한다. 최근에 개발된 타원 곡선 암호화기법은 타원곡선을 이용한 복잡한 문제를 기반으로 개발되었다. 위에 나열된 문제들은 어떤 수에 대한 모듈로(modular) 연산과 지수 연산 같은 것들을 기반으로 하기 때문에 전산학적으로 블록 사이퍼보다 시간이 오래걸린다. 따라서 공개키 암호체계는 주로 복합 암호체계(hybrid cryptosystems)를 사용하한다. 복합 암호체계선 주로 메세지를 암호화 속도가 빠른 대칭키 알고리즘을 이용해 암호화 하며 이 때 이용되는 키는 공개키 알고리즘을 이용해서 암호화 되어서 보내진다.
암호 해독학(Cryptanalysis)
암호 해독학의 가장 큰 목적은 암호 체계에서 보안상의 문제점이나 취약점을 발견해 이를 통해서 제 3자가 암호를 해독해 내는 것이다. 암호 해독은 주로 악의가 있는 공격자가 시스템을 파괴하기 위해 행해진다. 또는 그 시스템을 디자인한 사람이 자신의 시스템의 취약성을 파악하기 위해 공격하기도 한다. 현대에서는 암호화 알고리즘과 프로토콜들은 실제로 사용되기 전에 검사와 테스트를 거쳐서 높은 보안성이 검증 되면 사용한다.
일시패드(one-time-pad)
암호 해독을 하기 위해선 여러 종류의 방법이 사용되며 이는 다음과 같이 종류를 나눌 수 있다. 암호문 공격(ciphertext-only attack) 은 암호 해독가들이암호문들의 집합에만 오직 접근 가능하다는 것을 가정한 상태에서의 공격 방법이다.(현대의 좋은 암호체계는 이 암호문 공격에 당할 염려가 없다.) 알려진 평문 공격(known-plaintext attack)은 공격자가 평문과 암호문의 샘플을 가지고 있고 더 많은 정보(예를들자면 비밀키)를 알기위해 자유롭게 평문과 암호문에 대해 공격이 가능할 수 있는 공격 방법이다. 선택된 평문 공격(chosen-plaintext attack) 에서는 공격자가 평문과 이에 상응하는 암호문들을 가졌을 때의 공격방법이다. 한 예로 영국군이 독일군의 암호를 해독하기 위해 사용했던 Gardening 이란 작전도 이에 포함된다. 마지막으로 선택된 암호문 공격(chosen-ciphertext attack)은 공격자가 암호문을 고르고 이에 상응하는 평문을 알 때 사용하는 기법이다.
공개피 알고리즘은 앞에서 설명했듯이 전산학적으로 계산하기 힘든 문제에 기초를 둔다. 예를들자면 가장 유명한 것으로 큰 정수의 소인수 분해의 난해성(RSA 암호) 에 기초를 두거나 이산 대수문제의 난해성을 둔 암호들 도 있다. 따라서 공개키 암호의 해독은 컴퓨터를 통해서 더 빠르게, 효과적으로 계산하는 것이 필요하다. 예를들자면 현재까지 알려진 타원 곡선을 기반으로한 이산 대수 문제를 푸는 알고리즘은 현재까지 알려진 가장 빠른 소인수분해 알고리즘 보다 더 오래 걸리기 때문에 소인수분해 기반 사이퍼들은 타원 곡선 사이퍼 보다 더 큰 키를 이용한다. 따라서 계산 능력이 좀 떨어지는 소형 장비들은 RSA 암호보다 타원 곡선 암호를 이용하기 때문에 1990년대 중반 부터 유명세를 띄기 시작했다.
순수 암호 해독가들은 알고리즘 자체의 취약점을 이용해 암호를 해독하지만 다른 종류의 공격으로는 그 암호화 하는 장비 자체를 공격하는 것으로 'side-channel attacks' 라 부른다. 만약에 공격자가 예를들자면 장비가 암호화 할 평문들의 숫자에 접근이 가능하거나, 장비에게 비밀번호나 PIN 문자에 대한 오류 보고가 가능할 때, 공격자는 시이퍼를 뚫기 위한 타이밍 공격(timing attack) 이 가능하다. 또한 공격자가 중요 정보를 얻기 위해 전달되는 메세지 길이나, 패턴 등을 알아내는 것을 트래픽 분석(traffic analysis) 라 한다. 또한 그 암호하는 사람을 통해서 (절도, 강탈, 공갈, 간첩행위 등을 통해) 알아내는 방법도 있는데 여태까지 나열 한 방법 중 가장 효과적인 방법이라 볼 수 있다.
마치며...
암호학은 현대사회에서 매우 중요한 부분을 담당하고 있는 학문이다. 우리가 지금 인터넷을 쓰고 있는 상황에서도 수많은 정보가 부,복호화 되고 있으며 어디선가는 3자에 의해 해독되고 일지도 모른다(많은 수의 음모론자들은 NSA가 모두 도청해 해독한다고 한다). 뿐만 아니라 옥션 해킹 사건 처럼 보안에 대해서 취약한다면 자신의 개인정보가 모두 유출 될 지도 모른다. 따라서 우리는 암호학에 대한 관심을 가지고 보안에 신경써야 할 필요가 있다.
위 적은 내용(솔직히 번역한 나도 모르는 부분이 많다) 을 모두 알 필요는 없지만 암호사에 대한 간략한 내용과 우리가 쓰는 암호들의 종류, 그리고 전자 상거래 같은 중요한 기밀 자료 전달시에 사용되는 암호들이 무엇인지 아는 것은 필요하다고 생각한다.
참고자료
http://en.wikipedia.org/wiki/Cryptography (기본적으로 이 사이트의 내용을 통 번역했음)
그 외 사진을 찾은 수많은 인터넷 사이트들
우리말이 사전에 없는 단어들은 다른 사람이 쓴 단어를 사용함.
5/5 ~ 5/11 에 걸쳐 1주일간 번역함.
'Mathematics' 카테고리의 다른 글
| 비제네르 사이퍼(Vigenère cipher) 사용법과 그 해독법 (5) | 2008.05.11 |
|---|---|
| 빈도수 분석법(Frequency analysis) 를 이용한 암호 해독 (0) | 2008.05.11 |
| 여러가지 재미있는 풀이들 (0) | 2008.04.20 |
| 소수 (Prime number) 이야기 (7) | 2008.03.17 |
| 피타고라스 수 (Pythagorean triple) 와 그 해 (2) | 2008.02.20 |



