비제네르 사이퍼(Vigenère cipher) 사용법과 그 해독법
 '암호학(Cryptography)의 모든 것' 에서 비제네르 사이퍼(Vigenère cipher) 에 대해 간략하게 설명하고 있다. 비제네르 사이퍼란 다중단일문자치환 암호법의 한 종류로 키워드를 이용한 암호법이다. 이는 고전의 빈도수 분석법을 통해 쉽게 해독 될 수 있었던 고전 사이퍼와 달리 각 알파벳을 다른 알파벳으로 해독하며 키워드를 모른다면 해독하기에 힘들기 때문에 상당히 괜찮은 사이퍼라 할 수 있다. 그러나 키워드가 노출 된다면 해독은 매우 쉬워진다.
'암호학(Cryptography)의 모든 것' 에서 비제네르 사이퍼(Vigenère cipher) 에 대해 간략하게 설명하고 있다. 비제네르 사이퍼란 다중단일문자치환 암호법의 한 종류로 키워드를 이용한 암호법이다. 이는 고전의 빈도수 분석법을 통해 쉽게 해독 될 수 있었던 고전 사이퍼와 달리 각 알파벳을 다른 알파벳으로 해독하며 키워드를 모른다면 해독하기에 힘들기 때문에 상당히 괜찮은 사이퍼라 할 수 있다. 그러나 키워드가 노출 된다면 해독은 매우 쉬워진다.
비제네르 사이퍼를 통한 부,복호화는 말로 설명하기 힘드므로 아래의 예를 통해 보자.
우리가 'ATTACKATDAWN (새벽에 공격하자) ' 라는 평문을 비제네르 암호법을 통해 암호화 한다고 하자. 그러기 위해선 일단 키워드를 정해야 한다. 키워드로는 'LEMON' 을 택했다고 하자. 그렇다면 먼저 암호화 하려는 평문의 글자수에 맞게 키워드를 반복해 써준다.
이 때 우리가 알아야 할 사실은 각 알파벳에 숫자를 대응시킨다는 것이다. 즉, A는 0, B는 1, .... Z 는 25 까지 대응 되는 값을 가지고 있다. 이제 부호화 하기 위해 위 알파벳과 아래 알파벳(첫번째 열을 예를 들자면 L 과 A ) 를 더해준다. 즉 첫번째 열의 경우 L + A = 0 + 8 = 8 = L 이 된다. 이 때 만약 값이 26을 넘어간다면 모듈러 26을 취해 준 값( 즉 26으로 나눈 나머지. 예를들자면 Y+Z = 24 + 25 = 49 ≡ 23 (mod 26) 이므로 23 에 대응하는 X 가 된다. ) 에 대응하는 알파벳을 써 주면 된다.
따라서 암호화된 문장은 LXFOPVEFRNHR 이 된다. 만약 복호화 하고 싶다면 암호문에서 키워드를 빼 주면 된다.
비제네르 사이퍼가 만들어진 계기는 고전 사이퍼를 암호화 된 문장에 나타날 수 밖에 없었던 언어 통계학적인 문제(빈도수 분석법을 통해 쉽게 해독 될 수 있다.)를 가리기 위해서 였다. 예를들자면 고전 사이퍼로 암호화 된 문장에서 'P' 가 가장 많이 나타났다면 영어 알파벳 중 가장 많이 나타나는 것이 'e' 인 것을 보아 'P' 는 'e' 를 치환한 것이라 볼 수 있었다. 그러나 비제네르 사이퍼를 통해 암호화 된 암호문은 'P' 가 가장 많이 나타나더라도 각 알파벳은 서로 다른 알파벳으로 치환 될 수 있기 때문에 '무슨 알파벳이다' 라고 단정 짓기 힘들었다.
그러나 비제네르 사이퍼에도 문제가 있었다. 만약 키워드의 길이를 알아 낼 수 있다면 그 암호문은 카이사르 사이퍼가 독립적으로 엮여 있는 사이퍼와 똑같이 취급될 수 있기에 암호 해독이 너무나 쉬워진다. 따라서 키워드의 길이를 알아내기 위해 두 가지 테스트가 시행 될 수 있다. (반드시 알아낸다는 것은 아니다. )
첫번째 테스트로는 카지스키(Friedrich Kasiski) 방법으로 1863년에 개발되었으나, 실제로 1854년에 배비지(Charles Babbage) 는 이미 똑같은 테스트를 개발했었다. 카지스키 테스트는 암호문에서 똑같은 단어가 나오는 주기를 이용해 키워드의 길이를 찾는 것이다. 물론 운 좋게도 똑같은 낱말이 나올 수 도 있으나 그 확률은 희박하므로 대부분 똑같은 낱말이 나온다면 이 방법은 잘 먹혀들어간다.
카지스키 테스트는 암호문의 길이가 짧으면 별로 소용이 없지만(왜냐면 똑같은 두 단어가 나올 확률이 적으므로) 암호문의 길이가 길다면 똑같은 단어(영어단어에선 'the' 가 제일 많이 나온다. ) 가 나올 확률이 높아지므로 키워드의 길이를 찾을 확률이 높아진다.
두번째로 소개할 테스트는 프리드먼 테스트라 불리며 1920년에 프리드먼(William F. Friedman) 에 의해 개발되었다. 사이퍼의 글자 빈도수의 비균일성을 측정하기 위해 우연의 일치 지수(index of coincidence) 라는 것을 도입해 해독한다. 평문에서 무작위로 골라진 두 문자가 같아질 확률 κp (영어의 경우 0.067)와 일정하게 무작위로 고른 알파벳이 같아질 확률 κr 을(영어의 경우 0.0385) 이용하면 키워드의 길이는 다음과 같이 나타낼 수 있다.
다시한번 강조에서 말하지만 이 테스트를 통해 언제나 정확하게 키워드의 길이를 얻을 수 있는 것은 아니다. 또한 암호문의 길이가 짧으면 짧을 수록 정확성은 떨어지게 때문에 위 두 테스트가 모두 먹혀 들어가지 않는 암호문에 대해선 995115 개의 영어 단어를 하나하나씩 모두 해보는 수 밖에 없을지도 모른다.
다음 글을 읽어보기를 추천합니다. '암호학(Cryptography) 의 모든 것'

비제네르 사이퍼를 통한 부,복호화는 말로 설명하기 힘드므로 아래의 예를 통해 보자.
우리가 'ATTACKATDAWN (새벽에 공격하자) ' 라는 평문을 비제네르 암호법을 통해 암호화 한다고 하자. 그러기 위해선 일단 키워드를 정해야 한다. 키워드로는 'LEMON' 을 택했다고 하자. 그렇다면 먼저 암호화 하려는 평문의 글자수에 맞게 키워드를 반복해 써준다.
L E M O N L E M O N L E
A T T A C K A T D A W N
A T T A C K A T D A W N
이 때 우리가 알아야 할 사실은 각 알파벳에 숫자를 대응시킨다는 것이다. 즉, A는 0, B는 1, .... Z 는 25 까지 대응 되는 값을 가지고 있다. 이제 부호화 하기 위해 위 알파벳과 아래 알파벳(첫번째 열을 예를 들자면 L 과 A ) 를 더해준다. 즉 첫번째 열의 경우 L + A = 0 + 8 = 8 = L 이 된다. 이 때 만약 값이 26을 넘어간다면 모듈러 26을 취해 준 값( 즉 26으로 나눈 나머지. 예를들자면 Y+Z = 24 + 25 = 49 ≡ 23 (mod 26) 이므로 23 에 대응하는 X 가 된다. ) 에 대응하는 알파벳을 써 주면 된다.
L E M O N L E M O N L E
+ A T T A C K A T D A W N
= L X F O P V E F R N H R
+ A T T A C K A T D A W N
= L X F O P V E F R N H R
따라서 암호화된 문장은 LXFOPVEFRNHR 이 된다. 만약 복호화 하고 싶다면 암호문에서 키워드를 빼 주면 된다.
비제네르 사이퍼가 만들어진 계기는 고전 사이퍼를 암호화 된 문장에 나타날 수 밖에 없었던 언어 통계학적인 문제(빈도수 분석법을 통해 쉽게 해독 될 수 있다.)를 가리기 위해서 였다. 예를들자면 고전 사이퍼로 암호화 된 문장에서 'P' 가 가장 많이 나타났다면 영어 알파벳 중 가장 많이 나타나는 것이 'e' 인 것을 보아 'P' 는 'e' 를 치환한 것이라 볼 수 있었다. 그러나 비제네르 사이퍼를 통해 암호화 된 암호문은 'P' 가 가장 많이 나타나더라도 각 알파벳은 서로 다른 알파벳으로 치환 될 수 있기 때문에 '무슨 알파벳이다' 라고 단정 짓기 힘들었다.
그러나 비제네르 사이퍼에도 문제가 있었다. 만약 키워드의 길이를 알아 낼 수 있다면 그 암호문은 카이사르 사이퍼가 독립적으로 엮여 있는 사이퍼와 똑같이 취급될 수 있기에 암호 해독이 너무나 쉬워진다. 따라서 키워드의 길이를 알아내기 위해 두 가지 테스트가 시행 될 수 있다. (반드시 알아낸다는 것은 아니다. )
첫번째 테스트로는 카지스키(Friedrich Kasiski) 방법으로 1863년에 개발되었으나, 실제로 1854년에 배비지(Charles Babbage) 는 이미 똑같은 테스트를 개발했었다. 카지스키 테스트는 암호문에서 똑같은 단어가 나오는 주기를 이용해 키워드의 길이를 찾는 것이다. 물론 운 좋게도 똑같은 낱말이 나올 수 도 있으나 그 확률은 희박하므로 대부분 똑같은 낱말이 나온다면 이 방법은 잘 먹혀들어간다.
위에 굵게 표시된 부분 처럼 똑같은 부분이 반복해 나온다면 이 것의 주기(C~C 까지의) 를 계산해 키워드의 길이를 알 수 있다. 이 때 주기의 길이는 16이 나오니 키워드의 길이는 16의 약수인 2,4,8,16 중 하나일 것이다.키 : ABCDAB CD ABCDA BCD ABCDABCDABCD
평문 : CRYPTO IS SHORT FOR CRYPTOGRAPHY
암호문: CSASTP KV SIQUT GQU CSASTPIUAQJB
만약 위와 같은 암호문이 있다고 하자. 이 때, 'DYDUXRMH' 가 18의 주기를 가지고 나오므로 키워드의 길이는 18의 약수인 2,3,6,9,18 중 하나라 추정할 수 있다. 또한 NQD 가 20 의 주기를 가지고 나오므로 키워드의 길이는 2,4,5,10,20 중 하나라 추정할 수 있다. 이 때 공통된 2를 키워드의 길이라고 강력하게 확신 할 수 있다. (여기서 강력하다 라는 뜻은 운 좋게도 다른 단어이지만 똑같이 암호화 될 수 있기 때문에 반드시 주기를 가진다고 말할 수 없다.)암호문 : DYDUXRMHTVDVNQDQNWDYDUXRMHARTJGWNQD
카지스키 테스트는 암호문의 길이가 짧으면 별로 소용이 없지만(왜냐면 똑같은 두 단어가 나올 확률이 적으므로) 암호문의 길이가 길다면 똑같은 단어(영어단어에선 'the' 가 제일 많이 나온다. ) 가 나올 확률이 높아지므로 키워드의 길이를 찾을 확률이 높아진다.
두번째로 소개할 테스트는 프리드먼 테스트라 불리며 1920년에 프리드먼(William F. Friedman) 에 의해 개발되었다. 사이퍼의 글자 빈도수의 비균일성을 측정하기 위해 우연의 일치 지수(index of coincidence) 라는 것을 도입해 해독한다. 평문에서 무작위로 골라진 두 문자가 같아질 확률 κp (영어의 경우 0.067)와 일정하게 무작위로 고른 알파벳이 같아질 확률 κr 을(영어의 경우 0.0385) 이용하면 키워드의 길이는 다음과 같이 나타낼 수 있다.

이 때, κo 는 아래와 같이 나타내 진다.
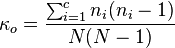
c 는 총 알파벳 수(영어의 경우 26) 이며, N 은 암호문의 길이, n1 부터 nc 는 암호문의 사이퍼 문자 빈도수를 가리킨다. 문장의 길이가 길면 길수록 이 테스트의 정확성은 높아진다.
다시한번 강조에서 말하지만 이 테스트를 통해 언제나 정확하게 키워드의 길이를 얻을 수 있는 것은 아니다. 또한 암호문의 길이가 짧으면 짧을 수록 정확성은 떨어지게 때문에 위 두 테스트가 모두 먹혀 들어가지 않는 암호문에 대해선 995115 개의 영어 단어를 하나하나씩 모두 해보는 수 밖에 없을지도 모른다.
다음 글을 읽어보기를 추천합니다. '암호학(Cryptography) 의 모든 것'
'Mathematics' 카테고리의 다른 글
| 페르마의 마지막 정리(Fermat's last theorem) 와 그 증명 (13) | 2008.05.15 |
|---|---|
| RSA 암호와 그 원리 (4) | 2008.05.12 |
| 빈도수 분석법(Frequency analysis) 를 이용한 암호 해독 (0) | 2008.05.11 |
| 암호학(Cryptography) 의 모든 것 (2) | 2008.05.11 |
| 여러가지 재미있는 풀이들 (0) | 2008.04.20 |



