빈도수 분석법(Frequency analysis) 를 이용한 암호 해독

  앞에서 '암호학(Cryptography) 의 모든 것' 을 통해 우리가 주로 쓰는 고전 사이퍼를 통해 부호화 된 암호문(환자식 암호법, 즉 각 알파벳을 다른 알파벳에 일대일 대응 시키는 것)을 풀 때 쓸 수 있다. 예를들자면 친구 끼리 서로 암호를 풀어보라고 쪽지를 주던가 아니면 퍼즐 문제 같은 경우도 고전 사이퍼를 이용해 암호화 된 암호문을 해독하라는 문제가 나올 때와 같은 경우에 빈도수 분석법을 효과적으로 쓸 수 있다.
  참고적으로 알아야 할 사실은 우리말에서는 환자식 암호법을 잘 쓰지 않는다. 왜냐하면 우리말은 '나' 라는 글자는 있을 수 있으나 'ㄱㅌㅣ' 라는 글자는 있을 수 없으므로 환자식 암호법으로 암호화 했을 시 '안녕' 을 'ㅈㅌㅍㅇㅣㅈ' 로 암호화 한다면 보기 이상하고 또 별로 좋지 않기 때문에 주로 영어를 쓸 때 위 사이퍼를 이용한다.

  빈도수 분석법은 통계학상으로 알파벳들이 쓰이는 회수가 똑같지 않다는 사실에 의거한다. 현재 까지 알려진 988,968 개의 영어 단어 중, 'e' 이 쓰이는 횟수는 13% 나 되지만 'z' 가 쓰이는 단어의 수는 0.01% 에도 미치지 못한다. 아래 그래프를 통해 더 확실히 볼 수 있을 것이다.

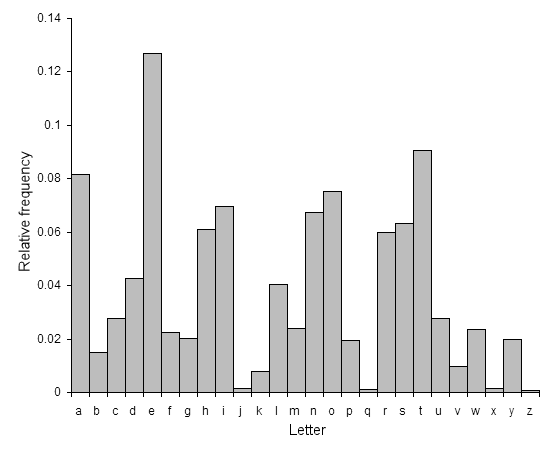
  따라서 어떠한 평문에서 'k' 가 많이 나타난다면 이는 'e' 를 'k' 로 치환했다고 볼 수 있을 것이다. 참 간단해 보이지만 실제론 쉽지 않다. 빈도수 분석은 통계학적인 사실에 의거하는 것이기 때문에 꼭 많이 나타난다고 해서 그 알파벳이 맞다고 볼 수 없기 때문이다. 결과적으로 빈도수 분석법을 통해 해독하려면 알파벳의 빈도수에 대한 뛰어난 관찰력과 엄청난 어휘력을 가지고 있어야 수월할 듯 하다.

  다음 암호문을 해독해 보며 한 번 빈도수 분석법이 어떻게 적용되는지 살펴보자.

LIVITCSWPIYVEWHEVSRIQMXLEYVEOIEWHRXEXIPFEMVEWHKVSTYLXZIXLIKIIXPIJ
VSZEYPERRGERIMWQLMGLMXQERIWGPSRIHMXQEREKIETXMJTPRGEVEKEITREW
HEXXLEXXMZITWAWSQWXSWEXTVEPMRXRSJGSTVRIEYVIEXCVMUIMWERGMIWX
MJMGCSMWXSJOMIQXLIVIQIVIXQSVSTWHKPEGARCSXRWIEVSWIIBXVIZMXFSJXLI
KEGAEWHEPSWYSWIWIEVXLISXLIVXLIRGEPIRQIVIIBGIIHMWYPFLEVHEWHYPSRRFQ
MXLEPPXLIECCIEVEWGISJKTVWMRLIHYSPHXLIQIMYLXSJXLIMWRIGXQEROIVFVIZE
VAEKPIEWHXEAMWYEPPXLMWYRMWXSGSWRMHIVEXMSWMGSTPHLEVHPFKPEZI
NTCMXIVJSVLMRSCMWMSWVIRCIGXMWYMX

  딱 보면 머리가 깨질 듯 하다. 하지만 자세히 살펴본다면 다음과 같은 사실을 볼 수 있다. 위 문장에서 XLI 가 세 글자 로는 (trigram, 삼자명)는 가장 많이 나타났다. (무려 9번이나. Ctrl-F 를 눌러 찾기를 이용하면 쉽게 알 수 있다.) 이 때, the 가 영어에서 가장 많이 쓰이는 세글자 단어인 것으로 보아 t 는 X 로 , h는  L로 , e는  I 로 각각 치환되었음을 볼 수 있다. 또한 위 암호문에서 'E' 는 무려 48이나 나타났으며, e 를 치환한 것은 'I' 인 것으로 보아, 두번째로 영어서 가장 많이 나타나는 'a' 인 것으로 미루어 볼 때, a 는 E 로 치환되었다고 볼 수 있다. 따라서 위 암호문을 정리해 보면

heVeTCSWPeYVaWHaVSReQMthaYVaOeaWHRtatePFaMVaWHKVSTYhtZetheKeetPeJ
VSZaYPaRRGaReMWQhMGhMtQaReWGPSReHMtQaRaKeaTtMJTPRGaVaKaeTRaW
HatthattMZeTWAWSQWtSWatTVaPMRtRSJGSTVReaYVeatCVMUeMWaRGMeWtMJMG
CSMWtSJOMeQtheVeQeVetQSVSTWHKPaGARCStRWeaVSWeeBtVeZMtFSJtheKaGAa
WHaPSWYSWeWeaVtheStheVtheRGaPeRQeVeeBGeeHMWYPFhaVHaWHYPSRRFQM
thaPPtheaCCeaVaWGeSJKTVWMRheHYSPHtheQeMYhtSJtheMWReGtQaROeVFVeZa
VAaKPeaWHtaAMWYaPPthMWYRMWtSGSWRMHeVatMSWMGSTPHhaVHPFKPaZeNT
CMteVJSVhMRSCMWMSWVeRCeGtMWYMt

가 된다. ( 참고로 대문자는 원래 암호문, 소문자는 원래 문자) 우리는 여기서 'Rtate' 가 쓰인 부분을 볼 수 있는데 'tate' 가 들어간 단어중 많이 쓰이는 단어로는 'state' 가 있으므로 s 가 R 로 치환되었음을 알 수 있따. 또한 'atthattMZe' 는 'atthattime' 즉, 'at that time' 을 치환한 것으로 쉽게 알 수 있다. 따라서 i 는 M 으로, m 은 Z 로 치환되었음을 알 수 있다. 또한 'heVe' 에서 'here' 을 치환 한 사실이라는 것도 쉽게 알 수 있다. 따라서 r 은 V 로 치환되었다.
또다시 정리해 보자면

hereTCSWPeYraWHarSseQithaYraOeaWHstatePFairaWHKrSTYhtmetheKeetPeJrSmaYP
assGaseiWQhiGhitQaseWGPSseHitQasaKeaTtiJTPsGaraKaeTsaWHatthattimeTWAWSQ
WtSWatTraPistsSJGSTrseaYreatCriUeiWasGieWtiJiGCSiWtSJOieQthereQeretQSrSTWH
KPaGAsCStsWearSWeeBtremitFSJtheKaGAaWHaPSWYSWeWeartheStherthesGaPesQ
ereeBGeeHiWYPFharHaWHYPSssFQithaPPtheaCCearaWGeSJKTrWisheHYSPHtheQei
YhtSJtheiWseGtQasOerFremarAaKPeaWHtaAiWYaPPthiWYsiWtSGSWsiHeratiSWiGSTP
HharHPFKPameNTCiterJSrhisSCiWiSWresCeGtiWYit

가 된다. 이 때, 'remarA' 에서 'remark' 가 치환되었다는 사실을 볼 수 있으므로 k 는 A 로 치환되었다. 또한 'thiWYs' 서 단어가 'thinks' 나 'things' 가 될 수 있지만 이미 k 는 A 로 치환됬다는 사실을 알고 있으므로 'things' 라는 사실도 알 수 있다. 따라서 n 은 W 로, g 는 Y 로 바뀌었다는 사실도 볼 수 있다. 정리해 보면

hereTCSnPegranHarSseQithagraOeanHstatePFairanHKrSTghtmetheKeetPeJrSmagPas
sGaseinQhiGhitQasenGPSseHitQasaKeaTtiJTPsGaraKaeTsanHatthattimeTnAnSQntSn
atTraPistsSJGSTrseagreatCriUeinasGientiJiGCSintSJOieQthereQeretQSrSTnHKPaGA
sCStsnearSneeBtremitFSJtheKaGAanHaPSngSneneartheStherthesGaPesQereeBGee
HingPFharHangPSssFQithaPPtheaCCearanGeSJKTrnisheHgSPHtheQeightSJtheinse
GtQasOerFremarkaKPeanHtaAingaPPthingsintSGSnsiHeratiSniGSTPHharHPFKPame
NTCiterJSrhisSCinSnresCeGtingit

가 된다. 이 때 'Qeight' 에서 이미 h 는 L 로 바뀌었음을 알고 있으므로 'height' 나 'weight'  둘 중 하나서 'weight' 가 된다. 따라서 w 는 Q 로 치환됬다. 또한 'inseGt' 에서 알맞은 단어론 'insert(삽입물)' 과 'insect(곤충)' 밖에 없는데 r 은 이미 V 로 치환되었으므로 'insect' 밖에 없다. 따라서 c 는 G 로 치환되었다.
마찬가지 방법으로 계속 찾아 본다면 다음과 같은 해독 된 문장을 얻을 수 있다.

hereuponlegrandarosewithagraveandstatelyairandbroughtmethebeetlefromaglasscasei
nwhichitwasencloseditwasabeautifulscarabaeusandatthattimeunknowntonaturalistsof
courseagreatprizeinascientificpointofviewthereweretworoundblackspotsnearoneextr
emityofthebackandalongoneneartheotherthescaleswereexceedinglyhardandglossywit
halltheappearanceofburnishedgoldtheweightoftheinsectwasveryremarkableandtaking
allthingsintoconsiderationicouldhardlyblamejupiterforhisopinionrespectingit

보기 좋게 띄어쓰기를 해본다면,

Here upon le grand arose with a grave and stately air and brought me the beetle 
from a glass case in which it was enclosed.  It was a beautiful scarabaeus and
at that time unknown to naturalists of course; a great prize in a scientific
point of view.  There were two round black spots near one extremity of the back
and a long one near the other.  The scales were exceedingly hard and glossy with
all the appearance of burnished gold.  The weight of the insect was very
remarkable and taking all things into consideration I could hardly blame jupiter
for his opinion respecting it.

과 같은 글이 완성된다.
  빈도수 분석법을 통해서 하나의 평문을 해독하려면 많은 시간이 걸리지만 요즘에서는 컴퓨터로 매우 빨리 해낼 수 있기 때문에 상관 없다. 빈도수 분석법 말고 26! 가지에 달하는 대응 가지수를 관찰 해 봐도 된다.

  빈도수 분석법은 고전 사이퍼를 통한 암호문에게는 효과적이지만 대칭키 사이퍼나, 공개키 사이퍼 같은 현대 암호 기술에게는 무력하다는 사실을 알고 있자.(똑같은 알파벳을 여러가지의 알파벳으로 암호화 하기 때문) 그렇지만 이거 하나 쯤은 알고있으면 좋을 듯 하다.

 '암호학(Cryptography) 의 모든 것' 을 아직 읽어보지 않았다면 읽기를 추천한다.