일반적으로 5차 이상의 방정식의 일반적인 해를 구할 수 없다는 사실은 잘 알려져 있다. 하지만 컴퓨터로 종종 5차 이상의 방정식의 해를 구할 필요가 생기게 된다. 이 때, 사람들은 뉴턴(Issac Newton) 과 랩슨(Joseph Raphson) 이 개발한 뉴턴-랩슨 법, 또는 그냥 뉴턴 법이라 알려진 방법을 이용하면 해의 근사치를 쉽게 구할 수 있다. 뉴튼 랩슨법은 상당히 단순함에도 불구하고 다항식의 해에 '매우 빠르게' 근접할 수 있다. 대부분의 경우 4 ~ 5회 정도 시행하게 된다면 10-⁴정도의 오차 내로 해를 구할 수 있게 된다.

어떤 함수 ƒ : [a, b] → R 가 구간 [a, b] 에서 미분 가능하다고 하자. (이 때, 이 함수의 해가 구간 [a,b] 안에 있다고 가정하자) 그렇다면 해로 추정되는 값 xn 을 생각할 수 있다. 따라서 xn 에서의 접선을 구해서 그 접선의 x 절편 xn+1 을 구한다면 그 점은 xn 보다 좀더 해에 근접하여 있을 것이다. (위 그림에 잘 나타나어 있다) 마찬가지 방법으로 위 작업을 계속 시행해 나간다면 결과적으로 위 함수 f 의 해 x 에 수렴하게 될 것이다.
(이 사실은 여기에 보면 잘 나타나 있다)
위 작업을 수식으로 표현한다면 아래와 같다.
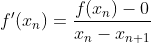
이 때, f'(x) 는 f(x) 의 1계 도함수 이다. 위 식을 다시 정리한다면
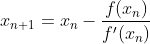
가 된다.
초기에 x0 를 어떻게 잡을 지는 큰 상관이 없다. 되도록 해에 근접한 값 일수록 해에 빠르게 가까워 지지만 구간 [a,b] 내 에서 어떠한 값을 잡아도 해를 구하는데 에는 큰 문자게 없다. 이 때 한 가지 주의해야 할 점은 ƒ'(x0) ≠ 0 가 되게 잡아야 한다.
자, 그럼 위 뉴튼 랩슨 법을 실제로 적용 시켜 보자.
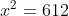
우리는 위 단순한 이차 방정식의 x 값을 뉴튼 랩슨법으로 구해보는 연습을 해 볼것이다. 일단, 위 방정식의 해 x 는 아래 함수의 해 라고 말할 수 있다.
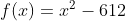
또한, 간단한 미분을 통해 위 함수 f 의 도함수 f' 를 구할 수 있다.
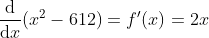
이 때, 위 f(x) 는 모든 실수에 대해 미분 가능하므로 굳이 구간을 따질 필요가 없다. 따라서, 초기의 값 x0 를 10 이라 하고 계산해 보자.
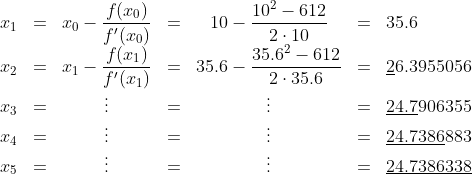
결과적으로 우리는 5 회만 계산했는데도 불구하고 위 방정식의 해를 소수점 7 번째 자리 까지 얻을 수 있었다. 보통 컴퓨터는 오차 이하 범위 까지 계산 한 후 계산을 중지한다.
뉴튼 랩슨 법은 다항 함수에 대해서만 적용되는 것이 아니라 다항 함수가 아니여도 조건들을 만족한다면 똑같은 방법으로 해를 구할 수 있다. 이번에는 cos x = x3 의 해를 구해 보도록 하자. 이는 아래 함수의 해 이다.
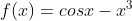
우리는 cos x 의 범위가 -1 부터 1 사이라는 것을 알고, 위 함수가 그 구간 내에서 미분 가능하다는 사실을 알고 있다. 또한 x > 1 이라면 x3 > 1 임을 알기 때문에 -1 < x < 1 이여야 하는 사실도 안다. 따라서 초기 값 x0 = 0.5 로 설정하자. 위 함수의 도함수를 구하면
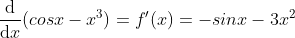
가 된다. 이 때 마찬가지 방법으로 뉴튼 랩슨 법을 적용 시킨다면
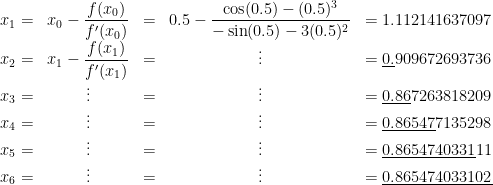
로 6 회 만에 소수점 13 자리 까지 매우 정확한 해를 구할 수 있게 된다.
뉴튼 랩슨 법을 사용시 반드시 주의해야 할 점은 일단 그 함수가 미분 가능한 것인지 판단해야 하며 (다항 함수는 모두 미분 가능하다), 시작점에서 값이 0 이 되지 않는지 꼭 체크해 주어야 정확한 해를 구할 수 있게 된다. (물론 시작점에서 값이 0 이 된다면 나눗셈 오류가 발생하겠지만..)

어떤 함수 ƒ : [a, b] → R 가 구간 [a, b] 에서 미분 가능하다고 하자. (이 때, 이 함수의 해가 구간 [a,b] 안에 있다고 가정하자) 그렇다면 해로 추정되는 값 xn 을 생각할 수 있다. 따라서 xn 에서의 접선을 구해서 그 접선의 x 절편 xn+1 을 구한다면 그 점은 xn 보다 좀더 해에 근접하여 있을 것이다. (위 그림에 잘 나타나어 있다) 마찬가지 방법으로 위 작업을 계속 시행해 나간다면 결과적으로 위 함수 f 의 해 x 에 수렴하게 될 것이다.
(이 사실은 여기에 보면 잘 나타나 있다)
위 작업을 수식으로 표현한다면 아래와 같다.
이 때, f'(x) 는 f(x) 의 1계 도함수 이다. 위 식을 다시 정리한다면
가 된다.
초기에 x0 를 어떻게 잡을 지는 큰 상관이 없다. 되도록 해에 근접한 값 일수록 해에 빠르게 가까워 지지만 구간 [a,b] 내 에서 어떠한 값을 잡아도 해를 구하는데 에는 큰 문자게 없다. 이 때 한 가지 주의해야 할 점은 ƒ'(x0) ≠ 0 가 되게 잡아야 한다.
자, 그럼 위 뉴튼 랩슨 법을 실제로 적용 시켜 보자.
우리는 위 단순한 이차 방정식의 x 값을 뉴튼 랩슨법으로 구해보는 연습을 해 볼것이다. 일단, 위 방정식의 해 x 는 아래 함수의 해 라고 말할 수 있다.
또한, 간단한 미분을 통해 위 함수 f 의 도함수 f' 를 구할 수 있다.
이 때, 위 f(x) 는 모든 실수에 대해 미분 가능하므로 굳이 구간을 따질 필요가 없다. 따라서, 초기의 값 x0 를 10 이라 하고 계산해 보자.
결과적으로 우리는 5 회만 계산했는데도 불구하고 위 방정식의 해를 소수점 7 번째 자리 까지 얻을 수 있었다. 보통 컴퓨터는 오차 이하 범위 까지 계산 한 후 계산을 중지한다.
뉴튼 랩슨 법은 다항 함수에 대해서만 적용되는 것이 아니라 다항 함수가 아니여도 조건들을 만족한다면 똑같은 방법으로 해를 구할 수 있다. 이번에는 cos x = x3 의 해를 구해 보도록 하자. 이는 아래 함수의 해 이다.
우리는 cos x 의 범위가 -1 부터 1 사이라는 것을 알고, 위 함수가 그 구간 내에서 미분 가능하다는 사실을 알고 있다. 또한 x > 1 이라면 x3 > 1 임을 알기 때문에 -1 < x < 1 이여야 하는 사실도 안다. 따라서 초기 값 x0 = 0.5 로 설정하자. 위 함수의 도함수를 구하면
가 된다. 이 때 마찬가지 방법으로 뉴튼 랩슨 법을 적용 시킨다면
로 6 회 만에 소수점 13 자리 까지 매우 정확한 해를 구할 수 있게 된다.
뉴튼 랩슨 법을 사용시 반드시 주의해야 할 점은 일단 그 함수가 미분 가능한 것인지 판단해야 하며 (다항 함수는 모두 미분 가능하다), 시작점에서 값이 0 이 되지 않는지 꼭 체크해 주어야 정확한 해를 구할 수 있게 된다. (물론 시작점에서 값이 0 이 된다면 나눗셈 오류가 발생하겠지만..)
'Mathematics' 카테고리의 다른 글
| 정다면체는 왜 5 개 밖에 없는가? (20) | 2009.07.17 |
|---|---|
| 체비셰프의 정리 (베르트랑 공준, Betrand Postulate) (7) | 2009.04.20 |
| 라그랑즈의 네제곱수 정리와 그 증명(Four square theorem) (4) | 2009.04.19 |
| 3차방정식의 근의 공식( 카르다노의 해법) 과 판별식 (21) | 2009.04.19 |
| 4차 방정식(Quartic Equation)의 페라리의 해법과 근의 공식 (4) | 2008.08.09 |



