여러가지 소수 ( Prime number ) 들
소수라고 하면, 약수(자연수인 약수만 따진다면)가 1과 그 자신밖에 없는 수를 일컫는다.
보통 유명한 소수들 하면, 메르센느 소수 라든지 페르마 소수 등 이 있는데, 이번 글에서는 정말 여러가지 종류의 이름이 붙은 소수들을 소개하고자 한다.
Balanced primes ( 균형잡힌(?) 소수 )
그 전 소수와 그 다음소수의 평균이 소수가 되는 수.
즉, 소수들만 모아놓은 수열 {Pn} 이 있을 때,
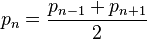을 만족하는 소수 Pn 을 균형잡힌 소수라 한다.
예를들어서 소수 53은 그 전 소수 47과 그 다음 소수 59의 평균이므로 균형잡힌 소수이다.
( OEIS의 A006562번 수열에서 확인 할 수 있다. )
균형잡힌 소수들의 종류로는
5, 53, 157, 173, 211, 257, 263, 373, 563, 593, 607, 653, 733, 947, 977, 1103, 1123, 1187, 1223, 1367, 1511, 1747, 1753, 1907, 2287, 2417, 2677, 2903, 2963, 3307, 3313, 3637, 3733 등이 있다.
Bell number primes ( 벨 수 소수 )
벨 수 는, 수학자 Eric Temple Bell 에서 따온 이름으로, 조합론에서 n 개의 원소로 구성되어 있는 집합을 분할하는 방법을 나타내며, 몇 가지 벨 수는 다음과 같다. 1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975 등 이 있다.
이 때, 이 벨 수 들 중에서 소수인 것들을 벨 수 소수 라 한다. 처음 몇 벨 수 소수로는
2, 5, 877, 27644437, 35742549198872617291353508656626642567, 359334085968622831041960188598043661065388726959079837
등이 있으며, 이는 OEIS 의 A051130 번 수열에서 찾을 수 있다.
Carol primes ( 캐롤 소수 )
크리스마스 캐롤이 아니다. ( 정확히 누구의 이름을 따왔는지는 모르겠다. )
이 캐롤 소수는 다음의 식을 만족하는 소수이다.
(2n − 1)2 − 2
처음 몇 캐롤 소수로는 7, 47, 223, 3967, 16127, 1046527, 16769023, 1073676287, 68718952447, 274876858367, 4398042316799, 1125899839733759, 18014398241046527 등이 있다.
Centered decagonal primes ( 딱히 한국말로 뭐라 할 지 모르겠다. 십각 소수(?) )
다음을 만족하는 소수다.
(5(n2 − n)) + 1
다음 식만 만족하는 수 들은 1, 11, 31, 61, 101, 151, 211, 281, 361, 451,551, 661, 781, 911, 1051, 등이 있으며, 이 들 중, 소수 인 것을 바로 Centered decagonal number 이라 한다.
이 십각수의 특징은 다음 그림의 구슬들의 개수를 이룬다. 즉, 가운데 구슬이 하나 있고 그 주위를 10각형이, 그 주위를 20각형이 ... 이렇게 둘러 쌓아낳아가는 수이다.
11, 31, 61, 101, 151, 211, 281, 661, 911, 1051, 1201, 1361, 1531, 1901, 2311, 2531, 3001, 3251, 3511, 4651, 5281, 6301, 6661, 7411, 9461, 9901, 12251, 13781, 14851, 15401, 18301, 18911, 19531
Centered heptagonal primes ( 칠각 소수 )
이는 위 십각 소수와 똑같지만, 칠각형으로 둘러 쌓아나간다는 점이 다르다.
칠각수는 (7n2 − 7n + 2) / 2 식을 만족하는 수를 가리키며, 이들 중 소수들을 칠각 소수라 한다. 처음 몇 개의 칠각 소수들은 다음과 같다.
43, 71, 197, 463, 547, 953, 1471, 1933, 2647, 2843, 3697, 4663, 5741, 8233, 9283, 10781, 11173, 12391, 14561, 18397, 20483, 29303, 29947, 34651, 37493, 41203, 46691
Centered square primes ( 사각 소수 )
이는 위 십각소수나 칠각 소수와 같지만, 이는 사각형으로 둘러 쌓아나간다는 점이 다르다.
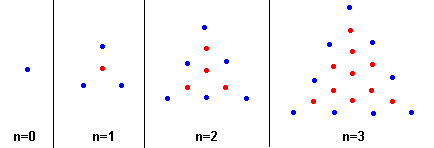
다음의 그림과 같이, 한 점을 중심으로 삼각형으로 덮어 나갈 때, 만족하는 점의 개수를 삼각수 (우리가 흔히 아는 삼각수가 아니라 딱히 Centered triangular primes 를 그냥 지어낸 말이다.)라고 하고, 이 삼각수들 중에 소수가 되는 수를 삼각 소수라 하자. 이는 (3n2 + 3n + 2) / 2 의 공식을 만족하기도 한다.
처음 몇 삼각수들을 나열해 보자면, 19, 31, 109, 199, 409, 571, 631, 829, 1489, 1999, 2341, 2971, 3529, 4621, 4789, 7039, 7669, 8779, 9721, 10459, 10711, 13681, 14851, 16069, 16381, 17659, 20011, 20359, 23251 등이 있다.
Chen primes ( 첸 소수 )
첸 소수는 어떤 소수 p 에 대해 p+2 가 소수거나 준소수 ( 두 소수의 곱으로 되어있는 소수, 예를들어 2의 제곱인 4나, 2×3 인 6 등이 준소수에 해당한다.) 일 경우 그 소수 p 를 첸 소수라 한다. 이때, 이 첸 소수가 무한하다는 것을 1966년 Chen Jingrun 이 증명하였다.
참고로 Rudolf Ondrejka 라는 사람이 첸 소수만으로 이루어진 3×3의 마방진을 발견하였다.
처음 몇 개의 첸 소수를 나열해 보자면
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 47, 53, 59, 67, 71, 83, 89, 101, 107, 109, 113, 127, 131, 137, 139, 149, 157, 167, 179, 181, 191, 197, 199, 211, 227, 233, 239, 251, 257, 263, 269 등이 있다.
Cousin primes ( 사촌 소수 )
마치 쌍둥이 소수 처럼 p 와 p+4 가 모두 소수인 소수 p , p+4 를 사촌 소수라 한다. 처음 몇 개의 사촌 소수들을 나열해 보자면 (3, 7), (7, 11), (13, 17), (19, 23), (37, 41), (43, 47), (67, 71), (79, 83), (97, 101), (103, 107), (109, 113), (127, 131), (163, 167), (193, 197), (223, 227), (229, 233), (277, 281) 등이 있다.
Cuban primes ( 쿠바 소수 )
다음 방정식을 만족하는 소수가 바로 쿠바 소수다.
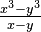, x = y + 1
이 방정식을 만족하는 소수들을 나열해 보자면 7, 19, 37, 61, 127, 271, 331, 397, 547, 631, 919, 1657, 1801, 1951, 2269, 2437, 2791, 3169, 3571, 4219, 4447, 5167, 5419, 6211, 7057, 7351, 8269, 9241, 10267, 11719, 12097, 13267, 13669 등이 있고,
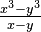, x = y + 2
이 방정식을 만족하는 소수들을 나열해 보자면, 13, 109, 193, 433, 769, 1201, 1453, 2029, 3469, 3889, 4801, 10093, 12289, 13873, 18253, 20173, 21169, 22189, 28813, 37633, 43201, 47629, 60493, 63949, 65713, 69313 이 있다.
Cullen primes ( 쿨렌 소수 )
쿨렌수는, Cn 으로 나타내며 1905년에 수학자 James Cullen 에 의해 처음 연구되었다. 이 때, 쿨렌수 Cn은 n · 2n + 1 와 같다. 이 때, 이 쿨렌수 들 중, 소수인 것을 바로 쿨렌 소수라 한다.
처음 몇 개의 쿨렌소수들을 나열해 보자면 3, 393050634124102232869567034555427371542904833 등이 있으며, 이는 각각 n 이 1 과 141 일 때 이다. 참고로 n 이 4713, 5795, 6611, 18496, 32292, 32469, 59656, 90825, 262419, 361275, 481899, 1354828 일 때 모두 Cn 은 쿨렌 소수이다. (숫자가 너무 커서 다 쓰지 못하겠다. )
Dihedral prime ( 숫자를 돌려도 소수가 나오는 소수 )
이 소수는 딱히 뭐라 부를 순 없고 뭐 거울소수(?) 라 불러야 적합하다. 이 소수는 어떤 소수를 돌려서 다시 소수가 나오면, Dihedral 소수라고 한다. 예를 들어서, 2 는 소수이지만 이를 돌리거나 대칭시키면 5 가 나오는데 이도 역시 소수므로 2와 5는 모두 Dihedral 소수이다.
처음 몇 개의 Dihedral 소수들을 나열해 보자면 2, 5, 11, 101, 181, 1181, 1811, 18181, 108881, 110881, 118081, 120121, 121021, 121151, 150151, 151051, 151121, 180181, 180811, 181081 등이 있고, 2006년에는 Phil Carmody 라는 사람이 10127576 + 1081101080188810801011801 × 1063776 + 1 인 가장 큰 Dihedral 소수를 찾았다.
Double Mersenne primes ( 복 메르센느 소수 )
p 가 소수일 때,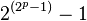
가 소수가 되면 이 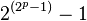는 복 메르센느 소수가 된다. 처음 몇가지 복 메르센느 소수를 나열해 보자면
어떤 소수 p 를 대칭시켜도 (예를들어 13을 대칭시키면 31) 소수가 나오는 소수 p 를 Emirps 소수라 한다. 처음 몇 개의 Emirps 소수를 나열해 보자면 13, 17, 31, 37, 71, 73, 79, 97, 107, 113, 149, 157, 167, 179, 199, 311, 337, 347, 359, 389, 701, 709, 733, 739, 743, 751, 761, 769, 907, 937, 941, 953, 967, 971, 983, 991 등이 있다.
Euclid primes ( 유클리드 소수 )
유클리드 수 En 을 En = pn# + 1 이라고 정의 할 때, ( 단, pn# 은 pn 이하의 모든 소수들의 곱이다 ), En 이 소수가 되면 이를 유클리드 소수라 하며 이는 그리스 수학자 유클리드가 En 꼴의 소수를 이용해 소수의 개수는 무한하다라는 증명한 것에서 유래하였다.
처음 몇 개의 유클리드 소수를 나열해 보자면, 3, 7, 31, 211, 2311, 200560490131 등이 있으며 모든 유클리드 수는 소수가 아니다. 예를들어, E6 = 13# + 1 = 30031 = 59 x 509 을 만족한다.
Even prime ( 짝수 소수 )
모두가 알듯이, 짝수인 소수는 2 밖에 없다. 한가지 유머로는 2를 가르켜 "the oddest prime" 라고 한다. ( 이는 영어로 odd 가 홀수라는 뜻 도 있지만 기괴하다는 뜻 도 있다. )
Factorial primes ( 계승 소수 )
n! − 1 또는 n! + 1 꼴을 만족하는 소수이다.
처음 몇 개의 계승소수들을 나열해 보자면, 2, 3, 5, 7, 23, 719, 5039, 39916801, 479001599, 87178291199, 10888869450418352160768000001, 265252859812191058636308479999999, 263130836933693530167218012159999999, 8683317618811886495518194401279999999 등이 있다.
Fermat primes ( 페르마 소수 )
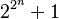의 꼴의 소수를 페르마 소수라 한다. 이는 페르마가 발견한 수로, 처음 F0,...,F4 의 페르마 수들은 쉽게 소수임을 보일 수 있지만 ( 계산해서 ) 그 다음부터는 복잡해 지는데, 페르마는 모든 페르마 수들이 소수라고 추측했다. 하지만 1732년 레온하르드 오일러에 의해
가 소수가 아님을 보여 페르마의 추론이 틀림을 보였다.
Fibonacci primes ( 피보나치 소수 )
피보나치 수열 { Fn } 을 F0 = 0, F1 = 1, Fn = Fn-1 + Fn-2 만족하는 수열로 정의할 때, 어떠한 자연수 n 에 대해 Fn 이 소수라면 이를 피보나치 소수라고 한다.
처음 몇 개의 피보나치 소수로는 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, 433494437, 2971215073, 99194853094755497, 1066340417491710595814572169, 19134702400093278081449423917 등이 있다.
Genocchi primes ( Genocchi 소수 )
Genocchi 수 Gn 는 다음을 만족하는 수 이다.
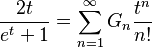
이 때, Gn 중 소수인 것을 Genocchi 소수라 하며, 17 밖에 없다.
Happy primes ( 좋은 소수 )
일단 Happy number , 즉 좋은 수 .는 다음과 같이 판별한다.
어떤 수를 골라서 각 자리를 제곱을 한 후 각각을 모두 더한다. 이때 새로나온 수의 각 자리를 제곱한 후, 다 더해 또 새로운 수를 만든다. 이 방법을 계속해 1이 되면 이 수는 좋은 수 이고, 1이 되지 않고 계속 똑같은 값이 순환이 되면 좋은 수가 아니다.
예를들어서 7이 좋은 수 인지 아닌지를 판별하려면
72 = 49
42 + 92 = 97
92 + 72 = 130
12 + 32 + 02 = 10
12 + 02 = 1 → 즉 7 은 좋은 수 이다.
컴퓨터의 계산에 따르면 1020 까지의 수들 중, 12% 정도는 좋은 수 라고 한다. 처음 몇 개의 좋은 수들을 나열해 보자면 1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100, 103, 109, 129, 130, 133, 139, 167, 176, 188, 190, 192, 193, 203, 208, 219, 226, 230, 236, 239, 262, 263, 280, 291, 293, 301, 302, 310, 313, 319, 320, 326, 329, 331, 338, 356, 362, 365, 367, 368, 376, 379, 383, 386, 391, 392, 397, 404, 409, 440, 446, 464, 469, 478, 487, 490, 496 등 이 있다. 이 때, 이들 중 소수인 것들이 바로 좋은 소수이다.
좋은 소수들을 나열해 보자면 7, 13, 19, 23, 31, 79, 97, 103, 109, 139, 167, 193, 239, 263, 293, 313, 331, 367, 379, 383, 397, 409, 487, 563, 617, 653, 673, 683, 709, 739, 761, 863, 881, 907, 937, 1009, 1033, 1039, 1093 등이 있다.
Higgs prime ( 힉스 소수 )
어떤 소수 p 에 대해, p-1 ( 또는 φ( p) ) 이 p 보다 작은 모든 힉스 소수의 제곱을 나눌 때, 소수 를 힉스소수라 한다. 이를 공식화 하면, 힉스소수 Hpn 은
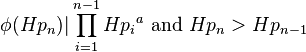
을 만족한다. 이 때, a=2 이다.
처음 몇 개의 힉스 소수를 나열해 보자면 2, 3, 5, 7, 11, 13, 19, 23, 29, 31, 37, 43, 47, 53, 59, 61, 67, 71, 79, 101, 107, 127, 131, 139, 149, 151, 157, 173, 181, 191, 197, 199, 211, 223, 229, 263, 269, 277, 283, 311, 317, 331, 347, 349 등 이 있다.
Kynea primes ( Kynea 소수 )
(2n + 1)2 − 2 꼴의 소수로 처음 몇개의 Kynea 소수를 나열해 보자면 7, 23, 79, 1087, 66047, 263167, 16785407, 1073807359, 17180131327, 68720001023, 4398050705407, 70368760954879, 18014398777917439, 18446744082299486207 등이 있다.
Left-truncatable primes ( 적당한 한국말은 없다. 딱히 부르자면, 왼쪽-제거 가능 소수 (?) )
이 소수는 제일 왼쪽의 자리수를 제거해도 계속 소수로 남아있는 소수를 일컫는다. 예를들어서 137에서 제일 왼쪽 1을 제거해도 37은 그대로 소수고, 37 또한 3을 제거해도 7 또한 소수므로 137은 Left-truncatable 소수이다.
처음 몇 개의 Left-truncatable 소수들을 나열해 보자면 2, 3, 5, 7, 13, 17, 23, 37, 43, 47, 53, 67, 73, 83, 97, 113, 137, 167, 173, 197, 223, 283, 313, 317, 337, 347, 353, 367, 373, 383, 397, 443, 467, 523, 547, 613, 617, 643, 647, 653, 673, 683 등 이 있다. Left-truncatable 소수는 총 4260개로 알려져 있으며, 가장 큰 것은 24자리 수 인, 357686312646216567629137 이다.
Leyland primes ( Leyland 소수 )
xy + yx , ( 1 < x ≤ y ) 의 꼴의 소수이며 처음 몇 개의 소수들을 나열해 보자면
17, 593, 32993, 2097593, 8589935681, 59604644783353249, 523347633027360537213687137, 43143988327398957279342419750374600193 등이 있으며 각각은 23+32, 29+92, 215+152, 221+212, 233+332, 524+245, 356+563, 1532+3215 에 대응한다. 2007년 1월에는 26384405 + 44052638 인 가장 큰 Leyland 소수가 발견되었다. 이는 2004년부터 2006년 말까지 타원곡선을 이용해 소수를 판별했으며, 이는 타원곡선을 이용해 소수를 판별한 가장 큰 소수가 되었다.
Long primes ( Long 소수 )
특정한 숫자 b 에 대해
의 값이 어떤 숫자를 반복한다면 이 때, 소수 p 를 Long 소수라고 한다. 보통은 b가 10일 때로 하며, b=10 때, Long 소수들을 나열해 보자면 7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, 179, 181, 193, 223, 229, 233, 257, 263, 269, 313, 337, 367, 379, 383, 389, 419, 433, 461, 487, 491, 499, 503, 509, 541, 571, 577, 593 등이 있다.
Lucas primes ( 루카스 소수 )
루카스 수열 {Ln } 을 L0 = 2, L1 = 1, Ln = Ln-1 + Ln-2 와 같이 정의할 때, 어떤 n 에 대해 Ln 이 소수가 되면 이 Ln 을 루카스 소수라 한다.
처음 몇 개의 루카스 소수들을 나열해 보자면 2, 3, 7, 11, 29, 47, 199, 521, 2207, 3571, 9349, 3010349, 54018521, 370248451, 6643838879, 119218851371, 5600748293801, 688846502588399, 32361122672259149 등이 있다.
Lucky primes ( 행운의 소수 )
행운의 소수는 행운의 수 중에서의 소수들을 일컫는다. 행운의수를 구하는 방법은 다음과 같다.
일단, 1 부터 시작하는 정수들을 나열한다.
1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25, ....
그 다음에 우리는 위 수열의 2번째에 위치한 수들을 지워나간다..
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25
이제, 위 수열의 2번째 항인 3, 즉 3번째의 위치한 수들, 즉 5,11 따위들을 지워나간다.
1, 3, 7, 9, 13, 15, 19, 21, 25, ....
이제, 위 수열의 3번째 항인 7, 즉 7번째에 위치한 수들을 지워나간다. 즉, 19 따위들을 지운다.
1, 3, 7, 9, 13, 15, 21, 25,
이제 위 수열의 4번째 항인 9, 즉 9번째에 위치한 수들을 지워나간다. 이러한 방식으로 구해서 걸러지지 않은 수들을 가리켜서 행운의 수라고 부른다. 이해가 되지 않았으면 다음의 애니메이션을 보아도 된다. ( 이 애니메이션을 만든 Celtic Minstrel 씨 에게 감사의 말을 전하고 싶군요 )
처음 몇 개의 행운의 수를 나열해 보자면 1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, 43, 49, 51, 63, 67, 69, 73, 75, 79, 87, 93, 99 등이 있고, 이들 중 소수인 것 만을 가르켜 행운의 소수라 한다. 처음 몇 개의 행운의 소수들을 나열하자면 3, 7, 13, 31, 37, 43, 67, 73, 79, 127, 151, 163, 193, 211, 223, 241, 283, 307, 331, 349, 367, 409, 421, 433, 463, 487, 541, 577, 601, 613, 619, 631, 643, 673, 727, 739, 769, 787, 823, 883, 937, 991, 997 등 이 있다.
Markov primes ( 마르코브 소수 )
마르코브 소수는 소수 p 에 대해 x2 + y2 + p2 = 3xyp 을 만족하는 정수 x,y 가 존재할 때, 소수 p 를 마르코브 소수라고 한다. 처음 몇 개의 마르코브 소수들을 나열해 보자면 2, 5, 13, 29, 89, 233, 433, 1597, 2897, 5741, 7561, 28657, 33461, 43261, 96557, 426389, 514229 등 이 있다.
Mersenne primes ( 메르센느 소수 )
메르센느 소수, 이름이 붙은 소수라면 가장 유명한 이 메르센느 소수는 n 번째 메르센느 소수를 가르켜 Mn 으로 나타내며, 이 Mn 은 Mn = 2n − 1 을 만족한다. 이는 17세기 프랑스의 학자 Marin Mersenne 의 이름을 따왔다.
메르센느 소수가 발견된 표는 아래와 같으며, n 은 2n − 1 의 n 을 의미한다.
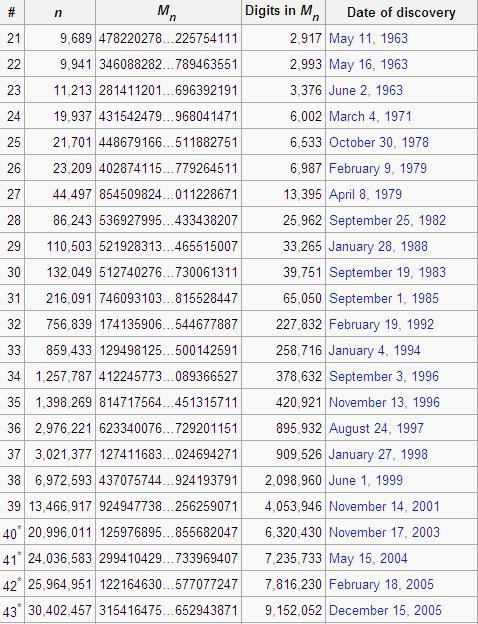
참고로 2007년 8월에는 9,808,358 자리의 44번째 메르센느 소수가 발견되었다. 처음 몇 개의 메르센느 소수를 나열하자면 3, 7, 31, 127, 8191, 131071, 524287, 2147483647, 2305843009213693951, 618970019642690137449562111, 162259276829213363391578010288127, 170141183460469231731687303715884105727 등 이 있다.
Padovan primes ( 파도반 소수 )
이는 파도반 수열 {P(n)} 을 P(0) = P(1) = P(2) = 1, P(n) = P(n − 2) + P(n − 3) 와 같이 정의할 때, 어떤 n 에 대해서 P(n) 이 소수이면 이를 파도반 소수 라 한다. 처음 몇 개의 파도반 소수를 나열하자면 2, 3, 5, 7, 37, 151, 3329, 23833, 13091204281, 3093215881333057, 1363005552434666078217421284621279933627102780881053358473 등이 있다.
Palindromic primes ( 대칭 소수 )
이 Palindromic 소수는 거꾸로 읽어도 똑같은 소수를 말한다. 예를들어서 131 같은 수는 거꾸로 읽어도 131로 똑같고 소수기 때문에 Palindromic 소수 이다. ( 대칭 소수라는 말은 없고 그냥 지어낸 말이다. ) 처음 몇 개의 Palindromic 소수로는 2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929, 10301, 10501, 10601, 11311, 11411, 12421, 12721, 12821, 13331, 13831, 13931, 14341, 14741 등 이 있다.
Pell primes ( 펠 소수 )
이는 펠 수열 {Pn } 을 P0 = 0, P1 = 1, Pn = 2Pn-1 + Pn-2 와 같이 정의할 때, 어떤 n 에 대해서 Pn 이 소수 이면 이를 펠 소수라 한다. 처음 몇 개의 펠 소수로는 2, 5, 29, 5741, 33461, 44560482149, 1746860020068409, 68480406462161287469, 13558774610046711780701, 4125636888562548868221559797461449 이 있다.
Permutable primes ( 순열 소수 )
이는 어떤 소수 p의 자릿수를 이용해서 만들 수 있는 모든 수 ( 예를들어 123 이라면 123 ,132, 213, 231, 312, 321) 이 모두 소수라면 이를 순열 소수 ( 이 것도 내가 만든 말이다. ) 라 한다. 처음 몇 개의 Permutable 소수를 나열해 보자면 2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, 97, 113, 131, 199, 311, 337, 373, 733, 919, 991, 1111111111111111111, 11111111111111111111111 등이 있고
Perrin primes ( 페린 소수 )
이는 페린 수열 {P(n)} 을 P(0) = 3, P(1) = 0, P(2) = 2, P(n) = P(n − 2) + P(n − 3) 와 같이 정의할 때, 어떤 수 n 에 대해 P(n) 이 소수이면 이를 페린 소수라 한다. 처음 몇 개의 페린 소수로는 2, 3, 5, 7, 17, 29, 277, 367, 853, 14197, 43721, 1442968193, 792606555396977, 187278659180417234321, 66241160488780141071579864797 이 있다.
Pierpont primes ( 피어폰트 소수 )
이는 임의의 정수 u,v ≥ 0 에 대해서, 어떤 소수 p 가 2u3v + 1 을 만족하면 이를 피어폰트 소수라 한다. 처음 몇 개의 피어폰트 소수로는 2, 3, 5, 7, 13, 17, 19, 37, 73, 97, 109, 163, 193, 257, 433, 487, 577, 769, 1153, 1297, 1459, 2593, 2917, 3457, 3889, 10369, 12289, 17497, 18433, 39367, 52489, 65537, 139969, 147457 등이 있으며, 현재까지 발견된 가장 큰 피어폰트 소수로는 2003년에 John Cosgrave, Paul Jobling, George Woltman, Yves Gallot 이 발견한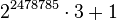
이 있다.
Pillai primes ( 필라이 소수 )
어떤 소수 p 가 n>0 이고, n 이 p-1 을 나누지 않을 때, n! + 1 을 나누는 정수 n 이 존재한다면 이 소수 p 는 필라이 소수이다. 처음 몇 개의 필라이 소수로는 23, 29, 59, 61, 67, 71, 79, 83, 109, 137, 139, 149, 193, 227, 233, 239, 251, 257, 269, 271, 277, 293, 307, 311, 317, 359, 379, 383, 389, 397, 401, 419, 431, 449, 461, 463, 467, 479, 499 등 이 있다.
Prime quadruplets ( 네쌍둥이 소수 )
(p, p+2, p+6, p+8) 가 모두 소수라면 이를 네쌍둥이 소수라 한다. 처음 몇 개의 네쌍둥이 소수로는 (5, 7, 11, 13), (11, 13, 17, 19), (101, 103, 107, 109), (191, 193, 197, 199), (821, 823, 827, 829), (1481, 1483, 1487, 1489), (1871, 1873, 1877, 1879), (2081, 2083, 2087, 2089), (3251, 3253, 3257, 3259), (3461, 3463, 3467, 3469), (5651, 5653, 5657, 5659), (9431, 9433, 9437, 9439) 등 이 있다.
Prime triplets ( 세쌍둥이 소수 )
(p, p+2, p+6) 또는 (p, p+4, p+6) 가 모두 소수인 소수를 가르켜 세쌍둥이 소수라 한다. 처음 몇 개의 세쌍둥이 소수로는 (5, 7, 11), (7, 11, 13), (11, 13, 17), (13, 17, 19), (17, 19, 23), (37, 41, 43), (41, 43, 47), (67, 71, 73), (97, 101, 103), (101, 103, 107), (103, 107, 109), (107, 109, 113), (191, 193, 197), (193, 197, 199), (223, 227, 229), (227, 229, 233), (277, 281, 283), (307, 311, 313), (311, 313, 317), (347, 349, 353) 등 이 있다.
Primorial primes ( Primorial 은 Prime 과 Factorial 이 합쳐진 단어로 한국말론 없는 단어 )
pn# − 1 or pn# + 1 꼴의 소수로 pn# 에 대한 정의는 위 유클리드 소수를 참고하기 바란다. 처음 몇 개의 Primorial 소수들을 나열하자면 3, 5, 7, 29, 31, 211, 2309, 2311, 30029, 200560490131, 304250263527209, 23768741896345550770650537601358309 이 있고, 2001년에는 Daniel Heuer 가 가장 큰 Primoral 소수 - 392113#+1 를 찾았다.
Proth primes ( 프로스 소수 )
k · 2n + 1 꼴의 소수 ( 단, k 는 홀수, k < 2n ) 를 가리켜 프로스 소수라 한다. 처음 몇 개의 프로스 소수를 나열하자면 3, 5, 13, 17, 41, 97, 113, 193, 241, 257, 353, 449, 577, 641, 673, 769, 929, 1153, 1217, 1409, 1601, 2113, 2689, 2753, 3137, 3329, 3457, 4481, 4993, 6529, 7297, 7681, 7937, 9473, 9601, 9857 이 있다.
Pythagorean primes ( 피타고라스 소수 )
이 피타코라스 소수는 4n + 1 꼴의 소수로 이는 직각삼각형의 빗변의 길이가 될 수 있다. 처음 몇 개의 피타고라스 소수를 나열하자면 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, 149, 157, 173, 181, 193, 197, 229, 233, 241, 257, 269, 277, 281, 293, 313, 317, 337, 349, 353, 373, 389, 397, 401, 409, 421, 433, 449 등 이 있다.
Repunit primes ( 반복 소수 )
이 소수는 숫자 1이 반복되는 소수로 처음 몇 개를 나열해 보자면 11, 1111111111111111111, 11111111111111111111111 등이 있고, 그 다음으로는 1이 317개와 1031개가 있다.
Right-truncatable primes ( 위의 Left-trunctable primes 와 같이 적당히 부를 말은 없다. )
이 소수는 위 Left-trunctable primes 와 같은 유형으로 이는 오른쪽을 한 자리씩 제거해도 모두 소수로 남아있는 수를 뜻한다. 예를들어 719는 소수이지만, 9를 제거한 71도 소수며, 1을 제거한 7 도 소수므로 719는 Right-truncatable 소수 이다. 처음 몇 개의 Right-truncatable 소수들을 나열하자면 2, 3, 5, 7, 23, 29, 31, 37, 53, 59, 71, 73, 79, 233, 239, 293, 311, 313, 317, 373, 379, 593, 599, 719, 733, 739, 797, 2333, 2339, 2393, 2399, 2939, 3119, 3137, 3733, 3739, 3793, 3797 이 있고 총 83개가 있다. 가장 큰 소수로는 8자리의 73939133 이다.
Safe prime ( 안전한 소수 )
이 안전한 소수는 p 과 (p-1) / 2 가 모두 소수임을 만족하는 소수로 Sophie Germain ( 소피 제르맹 ) 소수라고도 한다. 처음 몇 개의 안전한 소수를 나열하자면 5, 7, 11, 23, 47, 59, 83, 107, 167, 179, 227, 263, 347, 359, 383, 467, 479, 503, 563, 587, 719, 839, 863, 887, 983, 1019, 1187, 1283, 1307, 1319, 1367, 1439, 1487, 1523, 1619, 1823, 1907 등이 있다.
Smarandache-Wellin primes
이 Smarandache-Wellin 소수는 소수로만 구성되어있는 소수, 즉 2357(2,3,5,7 은 소수), 와 같은 소수를 가리킨다.처음 몇 개의 Smarandache-Wellin 소수를 나열해 보자면 2, 23, 2357 이 있고 그 다음은 128개의 소수가 붙어있는 꼴이다.
Star primes ( 스타 소수 )
이는 이 소수를 점으로 배열했을 때, 6선형 꼴의 모양이 나오는 소수이다. 즉, 위의 Centered decagonal 소수와 같은 형식의 소수이다. 6n(n - 1) + 1 의 식을 만족하며, 처음 몇 개의 스타 소수를 나열해 보자면 13, 37, 73, 181, 337, 433, 541, 661, 937, 1093, 2053, 2281, 2521, 3037, 3313, 5581, 5953, 6337, 6733, 7561, 7993, 8893, 10333, 10837, 11353, 12421, 12973, 13537, 15913, 18481 등 이 있다.
Super-prime ( 슈퍼 소수 )
소수 번째 소수이다. 즉, 2번째 소수,3번째 소수, 5번째 소수 들을 말한다. 예를들어서 7번째 소수 ( 7은 소수다 ) 17은 슈퍼 소수다. 하지만 4번째 소수 ( 4는 소수가 아니다.) 7은 슈퍼 소수가 아니다. 결과적으로 슈퍼 소수는 p(p(i)) 와 같이 나타내기도 한다. 처음 몇 개의 슈퍼 소수들을 나열해 보자면 3, 5, 11, 17, 31, 41, 59, 67, 83, 109, 127, 157, 179, 191, 211, 241, 277, 283, 331, 353, 367, 401, 431, 461, 509, 547, 563, 587, 599, 617, 709, 739, 773, 797, 859, 877, 919, 967, 991 등 이 있다.
Thabit number primes ( 싸비트 수 소수 )
이 소수는 3 · 2n - 1 꼴의 소수를 말한다. 처음 몇 개의 싸비트 소수로는 2, 5, 11, 23, 47, 191, 383, 6143, 786431, 51539607551, 824633720831, 26388279066623, 108086391056891903, 55340232221128654847, 226673591177742970257407 등이 있다.
Twin primes ( 쌍둥이 소수 )
(p, p + 2) 가 모두 소수이면 이를 쌍둥이 소수라 한다. 쌍둥이 소수에 관한 추론들은 아직 많이 증명되지 않았는데, 아직까지 쌍둥이 소수의 유/무한 성도 증명되지 않았다. 처음 몇 개의 쌍둥이 소수로는 (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463) 가 있으며, 현재까지 발견된 가장 큰 쌍둥이 소수로는 2003663613 · 2195000±1 이며 Eric Vautier 가 2005년 1월 15일에 발견하였다. 이 숫자는 58711 자리인 수 이다.
Ulam number primes ( Ulam 소수 )
이는 Ulam 수들 중 소수인 것을 가리킨다. Ulam 수는 Un 으로 나타내며 U1=1, U2=2 이다. 이는 앞에 나온 2개 숫자들의 합으로 나타낼 수 있는 가장 작은 수로, 그 수를 만들 수 있는 방법은 오직 한 가지여야만 한다. 처음 몇 개의 Ulam 수로는 1, 2, 3, 4, 6, 8, 11, 13, 16, 18, 26, 28, 36, 38, 47, 48, 53, 57, 62, 69, 72, 77, 82, 87, 97, 99 이 있다. ( 3=1+2,4=1+3, 2+2 는 용납 안됨. 5 가 Ulam 수가 되지 않는 이유는 5=2+3=1+4 이므로 2가지 방법으로 표현된다. 반면 6=2+4 로 밖에 표현이 되지 않으므로 4 다음에는 6이 온다. )
처음 몇 개의 Ulam 소수로는 2, 3, 11, 13, 47, 53, 97, 131, 197, 241, 409, 431, 607, 673, 739, 751, 983, 991, 1103, 1433, 1489 가 있다.
Wagstaff primes ( Wagstaff 소수 )
(2n + 1) / 3 꼴의 소수로 처음 몇 개를 나열해보자면 3, 11, 43, 683, 2731, 43691, 174763, 2796203, 715827883, 2932031007403, 768614336404564651, 201487636602438195784363, 845100400152152934331135470251, 56713727820156410577229101238628035243 이 있으며, 각각 n 이 3, 5, 7, 11, 13, 17, 19, 23, 31, 43, 61, 79, 101, 127, 167, 191, 199, 313, 347, 701, 1709, 2617, 3539, 5807, 10501, 10691, 11279, 12391, 14479, 42737, 83339, 95369, 117239, 127031, 138937, 141079, 267017, 269987, 374321 일 때 이다.
Wieferich primes ( Wieferich 소수 )
소수 p 에 대해 p2 이 2p − 1 − 1 를 나누면 이 소수 p 를 Wieferich 소수라 한다. 참고로 이 Wieferich 소수와 페르마의 마지막 정리는 연관성이 있다.p 를 소수라 하고, x,y,z 를 정수라 한다면 어떤 정수 x,y,z 에 대해 xp + yp + zp = 0 를 만족하고, p 가 x,y,z 의 곱을 나누지 않는다면 이 소수 p 는 Wieferich 소수이다. ( 참고로 이는 Wieferich 에 의해 1909년에 증명되었다 ). 현재까지 알려진 Wieferich 소수로는 1093, 3511 , 이 2개 밖에 없다.
Wilson primes ( 윌슨 소수 )
어떤 소수 p 에 대해 p2 이 (p − 1)! + 1를 나눈다면 이 소수 p 를 윌슨 소수라 하며 현재까지 알려진 윌슨 소수로는 5, 13, 563 , 이 3개 밖에 없다. 참고로 윌슨 소수가 무한하다는 것은 증명되지 않았고, 만약 더 있다면 이는 5 · 108 보다 클 것이다.
Woodall primes ( Woodall 소수 )
n · 2n − 1 꼴의 소수로 처음 몇 가지만 나열하자면 7, 23, 383, 32212254719, 2833419889721787128217599, 195845982777569926302400511, 4776913109852041418248056622882488319 가 있다.
이 사진은 메르센느 소수를 이진수로 쓴 것이다.
소수라고 하면, 약수(자연수인 약수만 따진다면)가 1과 그 자신밖에 없는 수를 일컫는다.
보통 유명한 소수들 하면, 메르센느 소수 라든지 페르마 소수 등 이 있는데, 이번 글에서는 정말 여러가지 종류의 이름이 붙은 소수들을 소개하고자 한다.
Balanced primes ( 균형잡힌(?) 소수 )
그 전 소수와 그 다음소수의 평균이 소수가 되는 수.
즉, 소수들만 모아놓은 수열 {Pn} 이 있을 때,
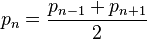을 만족하는 소수 Pn 을 균형잡힌 소수라 한다.예를들어서 소수 53은 그 전 소수 47과 그 다음 소수 59의 평균이므로 균형잡힌 소수이다.
( OEIS의 A006562번 수열에서 확인 할 수 있다. )
균형잡힌 소수들의 종류로는
5, 53, 157, 173, 211, 257, 263, 373, 563, 593, 607, 653, 733, 947, 977, 1103, 1123, 1187, 1223, 1367, 1511, 1747, 1753, 1907, 2287, 2417, 2677, 2903, 2963, 3307, 3313, 3637, 3733 등이 있다.
Bell number primes ( 벨 수 소수 )
벨 수 는, 수학자 Eric Temple Bell 에서 따온 이름으로, 조합론에서 n 개의 원소로 구성되어 있는 집합을 분할하는 방법을 나타내며, 몇 가지 벨 수는 다음과 같다. 1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975 등 이 있다.
이 때, 이 벨 수 들 중에서 소수인 것들을 벨 수 소수 라 한다. 처음 몇 벨 수 소수로는
2, 5, 877, 27644437, 35742549198872617291353508656626642567, 359334085968622831041960188598043661065388726959079837
등이 있으며, 이는 OEIS 의 A051130 번 수열에서 찾을 수 있다.
Carol primes ( 캐롤 소수 )
크리스마스 캐롤이 아니다. ( 정확히 누구의 이름을 따왔는지는 모르겠다. )
이 캐롤 소수는 다음의 식을 만족하는 소수이다.
(2n − 1)2 − 2
처음 몇 캐롤 소수로는 7, 47, 223, 3967, 16127, 1046527, 16769023, 1073676287, 68718952447, 274876858367, 4398042316799, 1125899839733759, 18014398241046527 등이 있다.
Centered decagonal primes ( 딱히 한국말로 뭐라 할 지 모르겠다. 십각 소수(?) )
다음을 만족하는 소수다.
(5(n2 − n)) + 1
다음 식만 만족하는 수 들은 1, 11, 31, 61, 101, 151, 211, 281, 361, 451,551, 661, 781, 911, 1051, 등이 있으며, 이 들 중, 소수 인 것을 바로 Centered decagonal number 이라 한다.
이 십각수의 특징은 다음 그림의 구슬들의 개수를 이룬다. 즉, 가운데 구슬이 하나 있고 그 주위를 10각형이, 그 주위를 20각형이 ... 이렇게 둘러 쌓아낳아가는 수이다.
아마 이 그림에 나와잇는 구슬들의 개수를 만족하는 수가 십각수, 그 들 중 소수가 십각소수이다.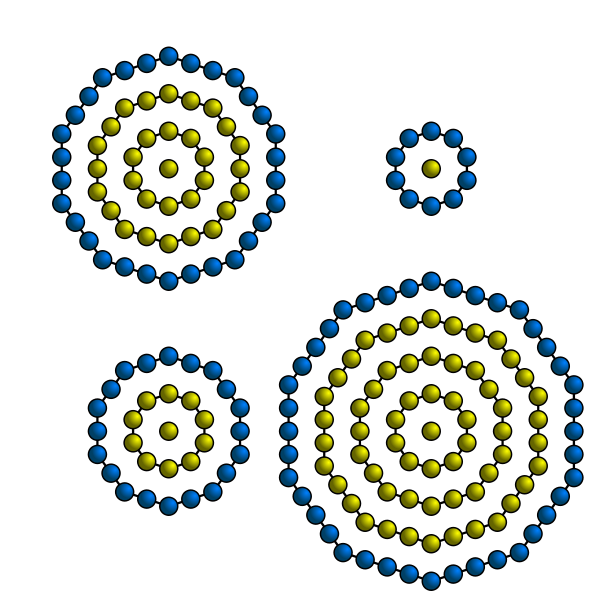
11, 31, 61, 101, 151, 211, 281, 661, 911, 1051, 1201, 1361, 1531, 1901, 2311, 2531, 3001, 3251, 3511, 4651, 5281, 6301, 6661, 7411, 9461, 9901, 12251, 13781, 14851, 15401, 18301, 18911, 19531
Centered heptagonal primes ( 칠각 소수 )
이는 위 십각 소수와 똑같지만, 칠각형으로 둘러 쌓아나간다는 점이 다르다.
칠각수는 (7n2 − 7n + 2) / 2 식을 만족하는 수를 가리키며, 이들 중 소수들을 칠각 소수라 한다. 처음 몇 개의 칠각 소수들은 다음과 같다.
43, 71, 197, 463, 547, 953, 1471, 1933, 2647, 2843, 3697, 4663, 5741, 8233, 9283, 10781, 11173, 12391, 14561, 18397, 20483, 29303, 29947, 34651, 37493, 41203, 46691
Centered square primes ( 사각 소수 )
이는 위 십각소수나 칠각 소수와 같지만, 이는 사각형으로 둘러 쌓아나간다는 점이 다르다.
 |
|
|
| |||
이는 다음의 그림을 만족하며, n2 + (n + 1)2 의 공식을 만족하는 소수 이기도 한다.
처음 몇 개의 사각 소수로는 5, 13, 41, 61, 113, 181, 313, 421, 613, 761, 1013, 1201, 1301, 1741, 1861, 2113, 2381, 2521, 3121, 3613, 4513, 5101, 7321, 8581, 9661, 9941, 10513, 12641, 13613, 14281, 14621 이 있다.
Centered triangular primes ( 삼각 소수 )
다음의 그림과 같이, 한 점을 중심으로 삼각형으로 덮어 나갈 때, 만족하는 점의 개수를 삼각수 (우리가 흔히 아는 삼각수가 아니라 딱히 Centered triangular primes 를 그냥 지어낸 말이다.)라고 하고, 이 삼각수들 중에 소수가 되는 수를 삼각 소수라 하자. 이는 (3n2 + 3n + 2) / 2 의 공식을 만족하기도 한다.
처음 몇 삼각수들을 나열해 보자면, 19, 31, 109, 199, 409, 571, 631, 829, 1489, 1999, 2341, 2971, 3529, 4621, 4789, 7039, 7669, 8779, 9721, 10459, 10711, 13681, 14851, 16069, 16381, 17659, 20011, 20359, 23251 등이 있다.
Chen primes ( 첸 소수 )
첸 소수는 어떤 소수 p 에 대해 p+2 가 소수거나 준소수 ( 두 소수의 곱으로 되어있는 소수, 예를들어 2의 제곱인 4나, 2×3 인 6 등이 준소수에 해당한다.) 일 경우 그 소수 p 를 첸 소수라 한다. 이때, 이 첸 소수가 무한하다는 것을 1966년 Chen Jingrun 이 증명하였다.
참고로 Rudolf Ondrejka 라는 사람이 첸 소수만으로 이루어진 3×3의 마방진을 발견하였다.
| 17 | 89 | 71 |
| 113 | 59 | 5 |
| 47 | 29 | 101 |
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 47, 53, 59, 67, 71, 83, 89, 101, 107, 109, 113, 127, 131, 137, 139, 149, 157, 167, 179, 181, 191, 197, 199, 211, 227, 233, 239, 251, 257, 263, 269 등이 있다.
Cousin primes ( 사촌 소수 )
마치 쌍둥이 소수 처럼 p 와 p+4 가 모두 소수인 소수 p , p+4 를 사촌 소수라 한다. 처음 몇 개의 사촌 소수들을 나열해 보자면 (3, 7), (7, 11), (13, 17), (19, 23), (37, 41), (43, 47), (67, 71), (79, 83), (97, 101), (103, 107), (109, 113), (127, 131), (163, 167), (193, 197), (223, 227), (229, 233), (277, 281) 등이 있다.
Cuban primes ( 쿠바 소수 )
다음 방정식을 만족하는 소수가 바로 쿠바 소수다.
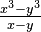, x = y + 1 이 방정식을 만족하는 소수들을 나열해 보자면 7, 19, 37, 61, 127, 271, 331, 397, 547, 631, 919, 1657, 1801, 1951, 2269, 2437, 2791, 3169, 3571, 4219, 4447, 5167, 5419, 6211, 7057, 7351, 8269, 9241, 10267, 11719, 12097, 13267, 13669 등이 있고,
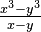, x = y + 2 이 방정식을 만족하는 소수들을 나열해 보자면, 13, 109, 193, 433, 769, 1201, 1453, 2029, 3469, 3889, 4801, 10093, 12289, 13873, 18253, 20173, 21169, 22189, 28813, 37633, 43201, 47629, 60493, 63949, 65713, 69313 이 있다.
Cullen primes ( 쿨렌 소수 )
쿨렌수는, Cn 으로 나타내며 1905년에 수학자 James Cullen 에 의해 처음 연구되었다. 이 때, 쿨렌수 Cn은 n · 2n + 1 와 같다. 이 때, 이 쿨렌수 들 중, 소수인 것을 바로 쿨렌 소수라 한다.
처음 몇 개의 쿨렌소수들을 나열해 보자면 3, 393050634124102232869567034555427371542904833 등이 있으며, 이는 각각 n 이 1 과 141 일 때 이다. 참고로 n 이 4713, 5795, 6611, 18496, 32292, 32469, 59656, 90825, 262419, 361275, 481899, 1354828 일 때 모두 Cn 은 쿨렌 소수이다. (숫자가 너무 커서 다 쓰지 못하겠다. )
Dihedral prime ( 숫자를 돌려도 소수가 나오는 소수 )
이 소수는 딱히 뭐라 부를 순 없고 뭐 거울소수(?) 라 불러야 적합하다. 이 소수는 어떤 소수를 돌려서 다시 소수가 나오면, Dihedral 소수라고 한다. 예를 들어서, 2 는 소수이지만 이를 돌리거나 대칭시키면 5 가 나오는데 이도 역시 소수므로 2와 5는 모두 Dihedral 소수이다.
처음 몇 개의 Dihedral 소수들을 나열해 보자면 2, 5, 11, 101, 181, 1181, 1811, 18181, 108881, 110881, 118081, 120121, 121021, 121151, 150151, 151051, 151121, 180181, 180811, 181081 등이 있고, 2006년에는 Phil Carmody 라는 사람이 10127576 + 1081101080188810801011801 × 1063776 + 1 인 가장 큰 Dihedral 소수를 찾았다.
Double Mersenne primes ( 복 메르센느 소수 )
p 가 소수일 때,
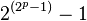가 소수가 되면 이 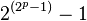는 복 메르센느 소수가 된다. 처음 몇가지 복 메르센느 소수를 나열해 보자면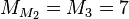 
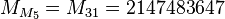
일 때에 각각이 모두 소수가 된다. 참고로 현재 2007년도 까지 이 4개들만 현재까지 알려진 복 메르센느 소수이며, p = 13, 17, 19, 31 때 에는 복 메르센느 소수가 아님이 밝혀졌다. 그 다음 메르센느 소수인 p=61 인 경우에 대해서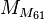 
의 값, 또는 22305843009213693951-1 이며, 이 조차 값이 너무 커서 (6.94×1017 자리) 확인이 거의 불가능 하다.
어떤 소수 p 를 대칭시켜도 (예를들어 13을 대칭시키면 31) 소수가 나오는 소수 p 를 Emirps 소수라 한다. 처음 몇 개의 Emirps 소수를 나열해 보자면 13, 17, 31, 37, 71, 73, 79, 97, 107, 113, 149, 157, 167, 179, 199, 311, 337, 347, 359, 389, 701, 709, 733, 739, 743, 751, 761, 769, 907, 937, 941, 953, 967, 971, 983, 991 등이 있다.
Euclid primes ( 유클리드 소수 )
유클리드 수 En 을 En = pn# + 1 이라고 정의 할 때, ( 단, pn# 은 pn 이하의 모든 소수들의 곱이다 ), En 이 소수가 되면 이를 유클리드 소수라 하며 이는 그리스 수학자 유클리드가 En 꼴의 소수를 이용해 소수의 개수는 무한하다라는 증명한 것에서 유래하였다.
처음 몇 개의 유클리드 소수를 나열해 보자면, 3, 7, 31, 211, 2311, 200560490131 등이 있으며 모든 유클리드 수는 소수가 아니다. 예를들어, E6 = 13# + 1 = 30031 = 59 x 509 을 만족한다.
Even prime ( 짝수 소수 )
모두가 알듯이, 짝수인 소수는 2 밖에 없다. 한가지 유머로는 2를 가르켜 "the oddest prime" 라고 한다. ( 이는 영어로 odd 가 홀수라는 뜻 도 있지만 기괴하다는 뜻 도 있다. )
Factorial primes ( 계승 소수 )
n! − 1 또는 n! + 1 꼴을 만족하는 소수이다.
처음 몇 개의 계승소수들을 나열해 보자면, 2, 3, 5, 7, 23, 719, 5039, 39916801, 479001599, 87178291199, 10888869450418352160768000001, 265252859812191058636308479999999, 263130836933693530167218012159999999, 8683317618811886495518194401279999999 등이 있다.
Fermat primes ( 페르마 소수 )
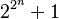의 꼴의 소수를 페르마 소수라 한다. 이는 페르마가 발견한 수로, 처음 F0,...,F4 의 페르마 수들은 쉽게 소수임을 보일 수 있지만 ( 계산해서 ) 그 다음부터는 복잡해 지는데, 페르마는 모든 페르마 수들이 소수라고 추측했다. 하지만 1732년 레온하르드 오일러에 의해 가 소수가 아님을 보여 페르마의 추론이 틀림을 보였다.Fibonacci primes ( 피보나치 소수 )
피보나치 수열 { Fn } 을 F0 = 0, F1 = 1, Fn = Fn-1 + Fn-2 만족하는 수열로 정의할 때, 어떠한 자연수 n 에 대해 Fn 이 소수라면 이를 피보나치 소수라고 한다.
처음 몇 개의 피보나치 소수로는 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, 433494437, 2971215073, 99194853094755497, 1066340417491710595814572169, 19134702400093278081449423917 등이 있다.
Genocchi primes ( Genocchi 소수 )
Genocchi 수 Gn 는 다음을 만족하는 수 이다.
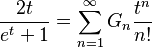
이 때, Gn 중 소수인 것을 Genocchi 소수라 하며, 17 밖에 없다.
Happy primes ( 좋은 소수 )
일단 Happy number , 즉 좋은 수 .는 다음과 같이 판별한다.
어떤 수를 골라서 각 자리를 제곱을 한 후 각각을 모두 더한다. 이때 새로나온 수의 각 자리를 제곱한 후, 다 더해 또 새로운 수를 만든다. 이 방법을 계속해 1이 되면 이 수는 좋은 수 이고, 1이 되지 않고 계속 똑같은 값이 순환이 되면 좋은 수가 아니다.
예를들어서 7이 좋은 수 인지 아닌지를 판별하려면
컴퓨터의 계산에 따르면 1020 까지의 수들 중, 12% 정도는 좋은 수 라고 한다. 처음 몇 개의 좋은 수들을 나열해 보자면 1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100, 103, 109, 129, 130, 133, 139, 167, 176, 188, 190, 192, 193, 203, 208, 219, 226, 230, 236, 239, 262, 263, 280, 291, 293, 301, 302, 310, 313, 319, 320, 326, 329, 331, 338, 356, 362, 365, 367, 368, 376, 379, 383, 386, 391, 392, 397, 404, 409, 440, 446, 464, 469, 478, 487, 490, 496 등 이 있다. 이 때, 이들 중 소수인 것들이 바로 좋은 소수이다.
좋은 소수들을 나열해 보자면 7, 13, 19, 23, 31, 79, 97, 103, 109, 139, 167, 193, 239, 263, 293, 313, 331, 367, 379, 383, 397, 409, 487, 563, 617, 653, 673, 683, 709, 739, 761, 863, 881, 907, 937, 1009, 1033, 1039, 1093 등이 있다.
Higgs prime ( 힉스 소수 )
어떤 소수 p 에 대해, p-1 ( 또는 φ( p) ) 이 p 보다 작은 모든 힉스 소수의 제곱을 나눌 때, 소수 를 힉스소수라 한다. 이를 공식화 하면, 힉스소수 Hpn 은
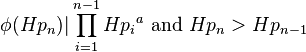
을 만족한다. 이 때, a=2 이다.
처음 몇 개의 힉스 소수를 나열해 보자면 2, 3, 5, 7, 11, 13, 19, 23, 29, 31, 37, 43, 47, 53, 59, 61, 67, 71, 79, 101, 107, 127, 131, 139, 149, 151, 157, 173, 181, 191, 197, 199, 211, 223, 229, 263, 269, 277, 283, 311, 317, 331, 347, 349 등 이 있다.
Kynea primes ( Kynea 소수 )
(2n + 1)2 − 2 꼴의 소수로 처음 몇개의 Kynea 소수를 나열해 보자면 7, 23, 79, 1087, 66047, 263167, 16785407, 1073807359, 17180131327, 68720001023, 4398050705407, 70368760954879, 18014398777917439, 18446744082299486207 등이 있다.
Left-truncatable primes ( 적당한 한국말은 없다. 딱히 부르자면, 왼쪽-제거 가능 소수 (?) )
이 소수는 제일 왼쪽의 자리수를 제거해도 계속 소수로 남아있는 소수를 일컫는다. 예를들어서 137에서 제일 왼쪽 1을 제거해도 37은 그대로 소수고, 37 또한 3을 제거해도 7 또한 소수므로 137은 Left-truncatable 소수이다.
처음 몇 개의 Left-truncatable 소수들을 나열해 보자면 2, 3, 5, 7, 13, 17, 23, 37, 43, 47, 53, 67, 73, 83, 97, 113, 137, 167, 173, 197, 223, 283, 313, 317, 337, 347, 353, 367, 373, 383, 397, 443, 467, 523, 547, 613, 617, 643, 647, 653, 673, 683 등 이 있다. Left-truncatable 소수는 총 4260개로 알려져 있으며, 가장 큰 것은 24자리 수 인, 357686312646216567629137 이다.
Leyland primes ( Leyland 소수 )
xy + yx , ( 1 < x ≤ y ) 의 꼴의 소수이며 처음 몇 개의 소수들을 나열해 보자면
17, 593, 32993, 2097593, 8589935681, 59604644783353249, 523347633027360537213687137, 43143988327398957279342419750374600193 등이 있으며 각각은 23+32, 29+92, 215+152, 221+212, 233+332, 524+245, 356+563, 1532+3215 에 대응한다. 2007년 1월에는 26384405 + 44052638 인 가장 큰 Leyland 소수가 발견되었다. 이는 2004년부터 2006년 말까지 타원곡선을 이용해 소수를 판별했으며, 이는 타원곡선을 이용해 소수를 판별한 가장 큰 소수가 되었다.
Long primes ( Long 소수 )
특정한 숫자 b 에 대해
의 값이 어떤 숫자를 반복한다면 이 때, 소수 p 를 Long 소수라고 한다. 보통은 b가 10일 때로 하며, b=10 때, Long 소수들을 나열해 보자면 7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, 179, 181, 193, 223, 229, 233, 257, 263, 269, 313, 337, 367, 379, 383, 389, 419, 433, 461, 487, 491, 499, 503, 509, 541, 571, 577, 593 등이 있다. Lucas primes ( 루카스 소수 )
루카스 수열 {Ln } 을 L0 = 2, L1 = 1, Ln = Ln-1 + Ln-2 와 같이 정의할 때, 어떤 n 에 대해 Ln 이 소수가 되면 이 Ln 을 루카스 소수라 한다.
처음 몇 개의 루카스 소수들을 나열해 보자면 2, 3, 7, 11, 29, 47, 199, 521, 2207, 3571, 9349, 3010349, 54018521, 370248451, 6643838879, 119218851371, 5600748293801, 688846502588399, 32361122672259149 등이 있다.
Lucky primes ( 행운의 소수 )
행운의 소수는 행운의 수 중에서의 소수들을 일컫는다. 행운의수를 구하는 방법은 다음과 같다.
일단, 1 부터 시작하는 정수들을 나열한다.
1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25, ....
그 다음에 우리는 위 수열의 2번째에 위치한 수들을 지워나간다..
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25
이제, 위 수열의 2번째 항인 3, 즉 3번째의 위치한 수들, 즉 5,11 따위들을 지워나간다.
1, 3, 7, 9, 13, 15, 19, 21, 25, ....
이제, 위 수열의 3번째 항인 7, 즉 7번째에 위치한 수들을 지워나간다. 즉, 19 따위들을 지운다.
1, 3, 7, 9, 13, 15, 21, 25,
이제 위 수열의 4번째 항인 9, 즉 9번째에 위치한 수들을 지워나간다. 이러한 방식으로 구해서 걸러지지 않은 수들을 가리켜서 행운의 수라고 부른다. 이해가 되지 않았으면 다음의 애니메이션을 보아도 된다. ( 이 애니메이션을 만든 Celtic Minstrel 씨 에게 감사의 말을 전하고 싶군요 )
행운의 수를 구하는 방법
처음 몇 개의 행운의 수를 나열해 보자면 1, 3, 7, 9, 13, 15, 21, 25, 31, 33, 37, 43, 49, 51, 63, 67, 69, 73, 75, 79, 87, 93, 99 등이 있고, 이들 중 소수인 것 만을 가르켜 행운의 소수라 한다. 처음 몇 개의 행운의 소수들을 나열하자면 3, 7, 13, 31, 37, 43, 67, 73, 79, 127, 151, 163, 193, 211, 223, 241, 283, 307, 331, 349, 367, 409, 421, 433, 463, 487, 541, 577, 601, 613, 619, 631, 643, 673, 727, 739, 769, 787, 823, 883, 937, 991, 997 등 이 있다.
Markov primes ( 마르코브 소수 )
마르코브 소수는 소수 p 에 대해 x2 + y2 + p2 = 3xyp 을 만족하는 정수 x,y 가 존재할 때, 소수 p 를 마르코브 소수라고 한다. 처음 몇 개의 마르코브 소수들을 나열해 보자면 2, 5, 13, 29, 89, 233, 433, 1597, 2897, 5741, 7561, 28657, 33461, 43261, 96557, 426389, 514229 등 이 있다.
Mersenne primes ( 메르센느 소수 )
메르센느 소수, 이름이 붙은 소수라면 가장 유명한 이 메르센느 소수는 n 번째 메르센느 소수를 가르켜 Mn 으로 나타내며, 이 Mn 은 Mn = 2n − 1 을 만족한다. 이는 17세기 프랑스의 학자 Marin Mersenne 의 이름을 따왔다.
메르센느 소수가 발견된 표는 아래와 같으며, n 은 2n − 1 의 n 을 의미한다.
참고로 2007년 8월에는 9,808,358 자리의 44번째 메르센느 소수가 발견되었다. 처음 몇 개의 메르센느 소수를 나열하자면 3, 7, 31, 127, 8191, 131071, 524287, 2147483647, 2305843009213693951, 618970019642690137449562111, 162259276829213363391578010288127, 170141183460469231731687303715884105727 등 이 있다.
Padovan primes ( 파도반 소수 )
이는 파도반 수열 {P(n)} 을 P(0) = P(1) = P(2) = 1, P(n) = P(n − 2) + P(n − 3) 와 같이 정의할 때, 어떤 n 에 대해서 P(n) 이 소수이면 이를 파도반 소수 라 한다. 처음 몇 개의 파도반 소수를 나열하자면 2, 3, 5, 7, 37, 151, 3329, 23833, 13091204281, 3093215881333057, 1363005552434666078217421284621279933627102780881053358473 등이 있다.
Palindromic primes ( 대칭 소수 )
이 Palindromic 소수는 거꾸로 읽어도 똑같은 소수를 말한다. 예를들어서 131 같은 수는 거꾸로 읽어도 131로 똑같고 소수기 때문에 Palindromic 소수 이다. ( 대칭 소수라는 말은 없고 그냥 지어낸 말이다. ) 처음 몇 개의 Palindromic 소수로는 2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929, 10301, 10501, 10601, 11311, 11411, 12421, 12721, 12821, 13331, 13831, 13931, 14341, 14741 등 이 있다.
Pell primes ( 펠 소수 )
이는 펠 수열 {Pn } 을 P0 = 0, P1 = 1, Pn = 2Pn-1 + Pn-2 와 같이 정의할 때, 어떤 n 에 대해서 Pn 이 소수 이면 이를 펠 소수라 한다. 처음 몇 개의 펠 소수로는 2, 5, 29, 5741, 33461, 44560482149, 1746860020068409, 68480406462161287469, 13558774610046711780701, 4125636888562548868221559797461449 이 있다.
Permutable primes ( 순열 소수 )
이는 어떤 소수 p의 자릿수를 이용해서 만들 수 있는 모든 수 ( 예를들어 123 이라면 123 ,132, 213, 231, 312, 321) 이 모두 소수라면 이를 순열 소수 ( 이 것도 내가 만든 말이다. ) 라 한다. 처음 몇 개의 Permutable 소수를 나열해 보자면 2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, 97, 113, 131, 199, 311, 337, 373, 733, 919, 991, 1111111111111111111, 11111111111111111111111 등이 있고
Perrin primes ( 페린 소수 )
이는 페린 수열 {P(n)} 을 P(0) = 3, P(1) = 0, P(2) = 2, P(n) = P(n − 2) + P(n − 3) 와 같이 정의할 때, 어떤 수 n 에 대해 P(n) 이 소수이면 이를 페린 소수라 한다. 처음 몇 개의 페린 소수로는 2, 3, 5, 7, 17, 29, 277, 367, 853, 14197, 43721, 1442968193, 792606555396977, 187278659180417234321, 66241160488780141071579864797 이 있다.
Pierpont primes ( 피어폰트 소수 )
이는 임의의 정수 u,v ≥ 0 에 대해서, 어떤 소수 p 가 2u3v + 1 을 만족하면 이를 피어폰트 소수라 한다. 처음 몇 개의 피어폰트 소수로는 2, 3, 5, 7, 13, 17, 19, 37, 73, 97, 109, 163, 193, 257, 433, 487, 577, 769, 1153, 1297, 1459, 2593, 2917, 3457, 3889, 10369, 12289, 17497, 18433, 39367, 52489, 65537, 139969, 147457 등이 있으며, 현재까지 발견된 가장 큰 피어폰트 소수로는 2003년에 John Cosgrave, Paul Jobling, George Woltman, Yves Gallot 이 발견한
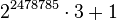이 있다.Pillai primes ( 필라이 소수 )
어떤 소수 p 가 n>0 이고, n 이 p-1 을 나누지 않을 때, n! + 1 을 나누는 정수 n 이 존재한다면 이 소수 p 는 필라이 소수이다. 처음 몇 개의 필라이 소수로는 23, 29, 59, 61, 67, 71, 79, 83, 109, 137, 139, 149, 193, 227, 233, 239, 251, 257, 269, 271, 277, 293, 307, 311, 317, 359, 379, 383, 389, 397, 401, 419, 431, 449, 461, 463, 467, 479, 499 등 이 있다.
Prime quadruplets ( 네쌍둥이 소수 )
(p, p+2, p+6, p+8) 가 모두 소수라면 이를 네쌍둥이 소수라 한다. 처음 몇 개의 네쌍둥이 소수로는 (5, 7, 11, 13), (11, 13, 17, 19), (101, 103, 107, 109), (191, 193, 197, 199), (821, 823, 827, 829), (1481, 1483, 1487, 1489), (1871, 1873, 1877, 1879), (2081, 2083, 2087, 2089), (3251, 3253, 3257, 3259), (3461, 3463, 3467, 3469), (5651, 5653, 5657, 5659), (9431, 9433, 9437, 9439) 등 이 있다.
Prime triplets ( 세쌍둥이 소수 )
(p, p+2, p+6) 또는 (p, p+4, p+6) 가 모두 소수인 소수를 가르켜 세쌍둥이 소수라 한다. 처음 몇 개의 세쌍둥이 소수로는 (5, 7, 11), (7, 11, 13), (11, 13, 17), (13, 17, 19), (17, 19, 23), (37, 41, 43), (41, 43, 47), (67, 71, 73), (97, 101, 103), (101, 103, 107), (103, 107, 109), (107, 109, 113), (191, 193, 197), (193, 197, 199), (223, 227, 229), (227, 229, 233), (277, 281, 283), (307, 311, 313), (311, 313, 317), (347, 349, 353) 등 이 있다.
Primorial primes ( Primorial 은 Prime 과 Factorial 이 합쳐진 단어로 한국말론 없는 단어 )
pn# − 1 or pn# + 1 꼴의 소수로 pn# 에 대한 정의는 위 유클리드 소수를 참고하기 바란다. 처음 몇 개의 Primorial 소수들을 나열하자면 3, 5, 7, 29, 31, 211, 2309, 2311, 30029, 200560490131, 304250263527209, 23768741896345550770650537601358309 이 있고, 2001년에는 Daniel Heuer 가 가장 큰 Primoral 소수 - 392113#+1 를 찾았다.
Proth primes ( 프로스 소수 )
k · 2n + 1 꼴의 소수 ( 단, k 는 홀수, k < 2n ) 를 가리켜 프로스 소수라 한다. 처음 몇 개의 프로스 소수를 나열하자면 3, 5, 13, 17, 41, 97, 113, 193, 241, 257, 353, 449, 577, 641, 673, 769, 929, 1153, 1217, 1409, 1601, 2113, 2689, 2753, 3137, 3329, 3457, 4481, 4993, 6529, 7297, 7681, 7937, 9473, 9601, 9857 이 있다.
Pythagorean primes ( 피타고라스 소수 )
이 피타코라스 소수는 4n + 1 꼴의 소수로 이는 직각삼각형의 빗변의 길이가 될 수 있다. 처음 몇 개의 피타고라스 소수를 나열하자면 5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, 137, 149, 157, 173, 181, 193, 197, 229, 233, 241, 257, 269, 277, 281, 293, 313, 317, 337, 349, 353, 373, 389, 397, 401, 409, 421, 433, 449 등 이 있다.
Repunit primes ( 반복 소수 )
이 소수는 숫자 1이 반복되는 소수로 처음 몇 개를 나열해 보자면 11, 1111111111111111111, 11111111111111111111111 등이 있고, 그 다음으로는 1이 317개와 1031개가 있다.
Right-truncatable primes ( 위의 Left-trunctable primes 와 같이 적당히 부를 말은 없다. )
이 소수는 위 Left-trunctable primes 와 같은 유형으로 이는 오른쪽을 한 자리씩 제거해도 모두 소수로 남아있는 수를 뜻한다. 예를들어 719는 소수이지만, 9를 제거한 71도 소수며, 1을 제거한 7 도 소수므로 719는 Right-truncatable 소수 이다. 처음 몇 개의 Right-truncatable 소수들을 나열하자면 2, 3, 5, 7, 23, 29, 31, 37, 53, 59, 71, 73, 79, 233, 239, 293, 311, 313, 317, 373, 379, 593, 599, 719, 733, 739, 797, 2333, 2339, 2393, 2399, 2939, 3119, 3137, 3733, 3739, 3793, 3797 이 있고 총 83개가 있다. 가장 큰 소수로는 8자리의 73939133 이다.
Safe prime ( 안전한 소수 )
이 안전한 소수는 p 과 (p-1) / 2 가 모두 소수임을 만족하는 소수로 Sophie Germain ( 소피 제르맹 ) 소수라고도 한다. 처음 몇 개의 안전한 소수를 나열하자면 5, 7, 11, 23, 47, 59, 83, 107, 167, 179, 227, 263, 347, 359, 383, 467, 479, 503, 563, 587, 719, 839, 863, 887, 983, 1019, 1187, 1283, 1307, 1319, 1367, 1439, 1487, 1523, 1619, 1823, 1907 등이 있다.
Smarandache-Wellin primes
이 Smarandache-Wellin 소수는 소수로만 구성되어있는 소수, 즉 2357(2,3,5,7 은 소수), 와 같은 소수를 가리킨다.처음 몇 개의 Smarandache-Wellin 소수를 나열해 보자면 2, 23, 2357 이 있고 그 다음은 128개의 소수가 붙어있는 꼴이다.
Star primes ( 스타 소수 )
이는 이 소수를 점으로 배열했을 때, 6선형 꼴의 모양이 나오는 소수이다. 즉, 위의 Centered decagonal 소수와 같은 형식의 소수이다. 6n(n - 1) + 1 의 식을 만족하며, 처음 몇 개의 스타 소수를 나열해 보자면 13, 37, 73, 181, 337, 433, 541, 661, 937, 1093, 2053, 2281, 2521, 3037, 3313, 5581, 5953, 6337, 6733, 7561, 7993, 8893, 10333, 10837, 11353, 12421, 12973, 13537, 15913, 18481 등 이 있다.
Super-prime ( 슈퍼 소수 )
소수 번째 소수이다. 즉, 2번째 소수,3번째 소수, 5번째 소수 들을 말한다. 예를들어서 7번째 소수 ( 7은 소수다 ) 17은 슈퍼 소수다. 하지만 4번째 소수 ( 4는 소수가 아니다.) 7은 슈퍼 소수가 아니다. 결과적으로 슈퍼 소수는 p(p(i)) 와 같이 나타내기도 한다. 처음 몇 개의 슈퍼 소수들을 나열해 보자면 3, 5, 11, 17, 31, 41, 59, 67, 83, 109, 127, 157, 179, 191, 211, 241, 277, 283, 331, 353, 367, 401, 431, 461, 509, 547, 563, 587, 599, 617, 709, 739, 773, 797, 859, 877, 919, 967, 991 등 이 있다.
Thabit number primes ( 싸비트 수 소수 )
이 소수는 3 · 2n - 1 꼴의 소수를 말한다. 처음 몇 개의 싸비트 소수로는 2, 5, 11, 23, 47, 191, 383, 6143, 786431, 51539607551, 824633720831, 26388279066623, 108086391056891903, 55340232221128654847, 226673591177742970257407 등이 있다.
Twin primes ( 쌍둥이 소수 )
(p, p + 2) 가 모두 소수이면 이를 쌍둥이 소수라 한다. 쌍둥이 소수에 관한 추론들은 아직 많이 증명되지 않았는데, 아직까지 쌍둥이 소수의 유/무한 성도 증명되지 않았다. 처음 몇 개의 쌍둥이 소수로는 (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463) 가 있으며, 현재까지 발견된 가장 큰 쌍둥이 소수로는 2003663613 · 2195000±1 이며 Eric Vautier 가 2005년 1월 15일에 발견하였다. 이 숫자는 58711 자리인 수 이다.
Ulam number primes ( Ulam 소수 )
이는 Ulam 수들 중 소수인 것을 가리킨다. Ulam 수는 Un 으로 나타내며 U1=1, U2=2 이다. 이는 앞에 나온 2개 숫자들의 합으로 나타낼 수 있는 가장 작은 수로, 그 수를 만들 수 있는 방법은 오직 한 가지여야만 한다. 처음 몇 개의 Ulam 수로는 1, 2, 3, 4, 6, 8, 11, 13, 16, 18, 26, 28, 36, 38, 47, 48, 53, 57, 62, 69, 72, 77, 82, 87, 97, 99 이 있다. ( 3=1+2,4=1+3, 2+2 는 용납 안됨. 5 가 Ulam 수가 되지 않는 이유는 5=2+3=1+4 이므로 2가지 방법으로 표현된다. 반면 6=2+4 로 밖에 표현이 되지 않으므로 4 다음에는 6이 온다. )
처음 몇 개의 Ulam 소수로는 2, 3, 11, 13, 47, 53, 97, 131, 197, 241, 409, 431, 607, 673, 739, 751, 983, 991, 1103, 1433, 1489 가 있다.
Wagstaff primes ( Wagstaff 소수 )
(2n + 1) / 3 꼴의 소수로 처음 몇 개를 나열해보자면 3, 11, 43, 683, 2731, 43691, 174763, 2796203, 715827883, 2932031007403, 768614336404564651, 201487636602438195784363, 845100400152152934331135470251, 56713727820156410577229101238628035243 이 있으며, 각각 n 이 3, 5, 7, 11, 13, 17, 19, 23, 31, 43, 61, 79, 101, 127, 167, 191, 199, 313, 347, 701, 1709, 2617, 3539, 5807, 10501, 10691, 11279, 12391, 14479, 42737, 83339, 95369, 117239, 127031, 138937, 141079, 267017, 269987, 374321 일 때 이다.
Wieferich primes ( Wieferich 소수 )
소수 p 에 대해 p2 이 2p − 1 − 1 를 나누면 이 소수 p 를 Wieferich 소수라 한다. 참고로 이 Wieferich 소수와 페르마의 마지막 정리는 연관성이 있다.p 를 소수라 하고, x,y,z 를 정수라 한다면 어떤 정수 x,y,z 에 대해 xp + yp + zp = 0 를 만족하고, p 가 x,y,z 의 곱을 나누지 않는다면 이 소수 p 는 Wieferich 소수이다. ( 참고로 이는 Wieferich 에 의해 1909년에 증명되었다 ). 현재까지 알려진 Wieferich 소수로는 1093, 3511 , 이 2개 밖에 없다.
Wilson primes ( 윌슨 소수 )
어떤 소수 p 에 대해 p2 이 (p − 1)! + 1를 나눈다면 이 소수 p 를 윌슨 소수라 하며 현재까지 알려진 윌슨 소수로는 5, 13, 563 , 이 3개 밖에 없다. 참고로 윌슨 소수가 무한하다는 것은 증명되지 않았고, 만약 더 있다면 이는 5 · 108 보다 클 것이다.
Woodall primes ( Woodall 소수 )
n · 2n − 1 꼴의 소수로 처음 몇 가지만 나열하자면 7, 23, 383, 32212254719, 2833419889721787128217599, 195845982777569926302400511, 4776913109852041418248056622882488319 가 있다.
'Mathematics' 카테고리의 다른 글
| 여러가지 재미있는 풀이들 (0) | 2008.04.20 |
|---|---|
| 소수 (Prime number) 이야기 (7) | 2008.03.17 |
| 피타고라스 수 (Pythagorean triple) 와 그 해 (2) | 2008.02.20 |
| 세계 각국의 수학 올림피아드 문제를 모아놓은 사이트 (1) | 2008.02.13 |
| 코시 - 슈바르쯔 부등식( Cauchy - Schwarz Inequality ) 과 그 증명 (2) | 2007.11.24 |
