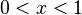여러가지 재미있는 풀이들
1. 1 = -1 이다.
이 문제의 경우 많은 (틀린)증명들이 있다. 한 번 살펴보자 .
방법 1
다음이 성립한다고 가정하자.
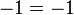
이 때, 위를 분수로 변형하면 아래와 같이 된다.
방법 3
그런데, abc = (ab)c 가 성립 하려면 a 가 양수여야 하지만 위의 경우 a 가 음수이므로 모순.
방법 4
다음은 삼각함수의 제곱관계를 이용한 증명이다.
일단 아래 식이 성립한다.
우리는 ab = ac 가 성립하면, b=c 임을 알 고 있다. 그런데 1x = 1y 이므로 x=y 이다.
이는 a=1 일 때 만 성립하므로 말이 안된다.
3. 루트 -1 은 1이다.
a,b 가 0이 아닐 때,
5. 0=1 이다.
다음과 같은 무한한 수열을 정의하자.
6. 모든 양수들의 합은 음수이다.
S 와 A 를 다음과 같이 정의하자.
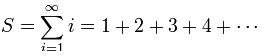
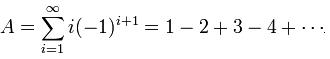
이 때, S-A = (1-1) + (2-(-2)) + (3-3) + .... = 4 + 8 + 12 + ... = 4S - ①
S+A = (1+1) + (2+(-2)) + (3+3) + .... = 2 + 6 + 10 + 14 + ... = 4S+(2+2+....) - ②
따라서 위의 ①, ② 식을 더하면
7. 모든 각의 크기는 0도 이다.
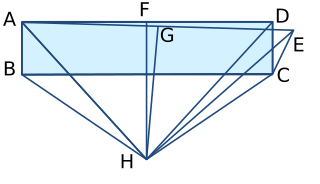
일단 직사각형 ABCD 를 잡자. 이 때 평면위에 DC = EC 인 점 E 를 잡자(단, ∠DCE=0 이 아니다. ) 이 때 선분 AD 의 중점 F 와 AE 의 중점 G 를 잡고 F 와 G 의 수선의 교점(즉, AD 와 AE 의 수직이등분선의 교점) 을 H 라 하자.
이 때, H 는 선분 AD의 수직이등분선위의 점이므로 AH 와 AD 가 같고 마찬가지로 AH 와 HE 가 같다. 따라서 DH 와 HE 는 같다. -> AH= DH = HE
또한 ABCD 가 직사각형 이므로 AB=DC 이고 DC=DE 인 점 E 를 잡았으므로
AB=DC=DE 이다. 마지막으로 AD,BC 가 평행하고 같으므로 선분 FH 는 BC 를 수직이등분 하므로 BH=CH 이다.
∴ Δ ABH ≡ Δ DCH ≡ Δ HCE (SSS) 이다.
∴ ∠DCH = ∠ ECH 이다. 그런데, ∠ECH = ∠DCH + ∠DCE 이므로 ∠DCE = 0 이다.
결과적으로 ∠DCE ≠ 0 = 0 -> 모든 각은 0 이다.
Q.E.D.
이 증명의 오류는 마지막 단계에서 나타난다. 위 그림을 정확하게 그린다면, ΔECH 의 모습은 직선 CH 에 대해 ΔDCH 의 반대쪽에 나타난다. 따라서 ∠ECH = ∠DCH + ∠DCE 이란 식은 아무 의미가 없다.
8. 1<0 이다.
일단 x 가 아래의 범위를 만족시킨다고 하자.
지금까지 황당한 결과를 내놓는 황당한 풀이들을 보았다. 나중에 수학에서 증명할 때 위와 같은 오류들(대표적으로 0으로 나눈다는 등...) 을 범하지 않도록 노력해야 한다.
참고로 내 개인적인 생각으로는 1은 1이다. 1은 0보다 작지도 않고 -1도, 0도 아니다.
1. 1 = -1 이다.
이 문제의 경우 많은 (틀린)증명들이 있다. 한 번 살펴보자 .
방법 1
다음이 성립한다고 가정하자.
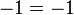
이 때, 위를 분수로 변형하면 아래와 같이 된다.

- 이 때, 양변에 루트를 씌운다면,
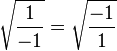
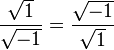
- 이제 양변을
 로 나누자.
로 나누자. -

- 모든 수(실수와 허수를 포함한) 의 대하여 그 수의 근호의 제곱은 원래 수를 도출하므로,
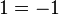
- Q.E.D.
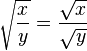
- 가 성립하려면, x,y 모두 양수 여야 한다.그런데 위의 경우 y 가 음수이므로 성립을 안한다.
- 방법 2

- Q.E.D.
- 이는 근호를 적절하게 변형해서 위와 같은 결론을 도출했는데,

방법 3
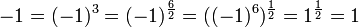
- Q.E.D.
그런데, abc = (ab)c 가 성립 하려면 a 가 양수여야 하지만 위의 경우 a 가 음수이므로 모순.
방법 4
다음은 삼각함수의 제곱관계를 이용한 증명이다.
일단 아래 식이 성립한다.

- 이 때 양변에 3/2 승을 취하면


- 이 때 x 가 π ( = 180 ) 일 때,
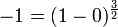

- 가 성립한다.
- Q.E.D.
- 그런데 이 역시 위 처럼 (ab)c = abc 가 성립하려면 a 가 양수여야 하는데 아니므로 모순.
우리는 ab = ac 가 성립하면, b=c 임을 알 고 있다. 그런데 1x = 1y 이므로 x=y 이다.
이는 a=1 일 때 만 성립하므로 말이 안된다.
3. 루트 -1 은 1이다.

- Q.E.D.
- 이 증명의 오류는 맨 마지막 변환에서 나타나는데, 1의 사제곱근은 1의 값을 가지기도 하지만, -1, i, -i 도 값으로 가지기 때문에 틀렸다.
a,b 가 0이 아닐 때,

- 가 성립한다고 하자. 이 때, 양변에 a 를 곱하면
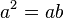
- 가 된다. 양변에서 b 를 빼주면

- 가 되고 인수분해를 하면,

- 가 된다. 이 때 양변을 a-b 로 나누면

- 이다. 그런데 위의 조건에서 a=b 이므로
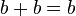

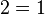
- 이다.
- Q.E.D.
5. 0=1 이다.
다음과 같은 무한한 수열을 정의하자.

- 이 때, 0 = 1-1 이므로
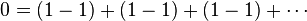
- 이 때, 위 수열을 다음과 같이 바꿀 수 있다.
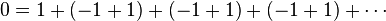
- 이 때 -1+1=0 이므로,
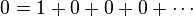
- 따라서

- Q.E.D.
6. 모든 양수들의 합은 음수이다.
S 와 A 를 다음과 같이 정의하자.
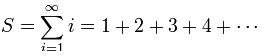
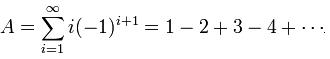
이 때, S-A = (1-1) + (2-(-2)) + (3-3) + .... = 4 + 8 + 12 + ... = 4S - ①
S+A = (1+1) + (2+(-2)) + (3+3) + .... = 2 + 6 + 10 + 14 + ... = 4S+(2+2+....) - ②
따라서 위의 ①, ② 식을 더하면

- 따라서 모든 양수들의 합은 음수이다.
- Q.E.D.
7. 모든 각의 크기는 0도 이다.

일단 직사각형 ABCD 를 잡자. 이 때 평면위에 DC = EC 인 점 E 를 잡자(단, ∠DCE=0 이 아니다. ) 이 때 선분 AD 의 중점 F 와 AE 의 중점 G 를 잡고 F 와 G 의 수선의 교점(즉, AD 와 AE 의 수직이등분선의 교점) 을 H 라 하자.
이 때, H 는 선분 AD의 수직이등분선위의 점이므로 AH 와 AD 가 같고 마찬가지로 AH 와 HE 가 같다. 따라서 DH 와 HE 는 같다. -> AH= DH = HE
또한 ABCD 가 직사각형 이므로 AB=DC 이고 DC=DE 인 점 E 를 잡았으므로
AB=DC=DE 이다. 마지막으로 AD,BC 가 평행하고 같으므로 선분 FH 는 BC 를 수직이등분 하므로 BH=CH 이다.
∴ Δ ABH ≡ Δ DCH ≡ Δ HCE (SSS) 이다.
∴ ∠DCH = ∠ ECH 이다. 그런데, ∠ECH = ∠DCH + ∠DCE 이므로 ∠DCE = 0 이다.
결과적으로 ∠DCE ≠ 0 = 0 -> 모든 각은 0 이다.
Q.E.D.
이 증명의 오류는 마지막 단계에서 나타난다. 위 그림을 정확하게 그린다면, ΔECH 의 모습은 직선 CH 에 대해 ΔDCH 의 반대쪽에 나타난다. 따라서 ∠ECH = ∠DCH + ∠DCE 이란 식은 아무 의미가 없다.
8. 1<0 이다.
일단 x 가 아래의 범위를 만족시킨다고 하자.

- 이 때 양변을 ln(x) 로 나누면
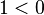
Q.E.D.
위 증명의 오류는 마지막 부분에 ln(x) 로 나누는 부분인데, 0 < x < 1 일 때, ln(x) 는 음수값을 가지므로 나누게 된다면 부등호의 방향이 바뀌면서 1>0 이된다.
지금까지 황당한 결과를 내놓는 황당한 풀이들을 보았다. 나중에 수학에서 증명할 때 위와 같은 오류들(대표적으로 0으로 나눈다는 등...) 을 범하지 않도록 노력해야 한다.
참고로 내 개인적인 생각으로는 1은 1이다. 1은 0보다 작지도 않고 -1도, 0도 아니다.
'Mathematics' 카테고리의 다른 글
| 빈도수 분석법(Frequency analysis) 를 이용한 암호 해독 (0) | 2008.05.11 |
|---|---|
| 암호학(Cryptography) 의 모든 것 (2) | 2008.05.11 |
| 소수 (Prime number) 이야기 (7) | 2008.03.17 |
| 피타고라스 수 (Pythagorean triple) 와 그 해 (2) | 2008.02.20 |
| 세계 각국의 수학 올림피아드 문제를 모아놓은 사이트 (1) | 2008.02.13 |