체비셰프
베르트랑의 공준에 따르면 2 이상의 자연수 n 에 대해, n < p < 2n 을 만족하는 소수 p 가 반드시 존재한다. 이는 최초로 체비셰프(Chebyshev)에 의해 증명되었으나 그의 증명인 길고 복잡하였다. 왜냐하면 체비셰프는 원래 이 문제를 증명한 것이 아니라 다른 문제를 해결하므로써 파생된 결과 이였기 때문이다. 후에 인도의 수학자 라마누잔(Ramanujan)이 쳬비셰프의 방법 보다 훨씬 간단한 방법으로 증명하였다. 하지만 나중에 폴 에르디시(Paul Erdős)가 기초적인 수학만을 사용하여 간결하게 증명하였는데, 여기 소개하고자 할 증명은 바로 폴 에르디시의 증명이다. (참고로 이 증명은 http://en.wikipedia.org/wiki/Proof_of_Bertrand%27s_postulate 에서 참조하였다. )
체비셰프의 정리
2 이상의 모든 자연수 n 에 대해서, n < p < 2n 을 만족하는 소수 p 가 존재한다.
2 이상의 모든 자연수 n 에 대해서, n < p < 2n 을 만족하는 소수 p 가 존재한다.
이 문제에 대해서는 보조정리가 5 개 필요하다.
증명)
일단, 이항정리에 따라
그런데,
증명)
그런데,
이면, 위 시그마 항들이 모두 0 이 된다. 또한,
n 이 짝수 일 때;
n > 2 이고, 짝수인 소수는 2 가 유일하므로
n 이 홀수 일 때;
이번 증명에서는 귀류법을 이용하자. 일단, n ≤ 2048 일 때, 3, 5, 7, 13, 23, 43, 83, 163, 317, 631, 1259, 2503 에 의해 성립. 따라서, n > 2048 일 때를 살펴보자.
어느 2048 보다 큰 임의의 자연수 n 에 대해, n < p < 2n 을 만족하는 소수가 존재하지 않음을 가정하자.
이 때, 아래의 조건을 만족하는 소수 p 를 생각하자.
따라서, p | \binom{2n}{n} 를 만족하는 모든 소수 p 는 p ≤ 2n / 3 을 만족한다.
이 때, 보조정리 2 에 의해 다음과 같이 될 수 있다.
또한, 보조정리 1 에 의해
이고, 보조정리 4 에 의해
따라서, 위 세 식에 의해 다음이 성립한다.
위 식을 정리하면
이 때, 보조정리 5 - 2,3 에 의하여
양변에 로그를 취하면
이 때, 보조정리 2 에 의해 다음과 같이 될 수 있다.
또한, 보조정리 1 에 의해
이고, 보조정리 4 에 의해
따라서, 위 세 식에 의해 다음이 성립한다.
위 식을 정리하면
이 때, 보조정리 5 - 2,3 에 의하여
양변에 로그를 취하면
'Mathematics' 카테고리의 다른 글
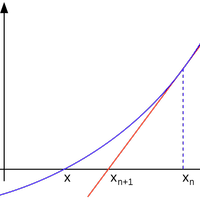
| 고차 방정식의 해 구하기 (뉴튼 - 랩슨법, Newton-Rahpson Method) (9) | 2009.09.27 |
|---|---|
| 정다면체는 왜 5 개 밖에 없는가? (20) | 2009.07.17 |
| 라그랑즈의 네제곱수 정리와 그 증명(Four square theorem) (4) | 2009.04.19 |
| 3차방정식의 근의 공식( 카르다노의 해법) 과 판별식 (21) | 2009.04.19 |
| 4차 방정식(Quartic Equation)의 페라리의 해법과 근의 공식 (4) | 2008.08.09 |